Vectors Pt. 3

Created Thursday 04 June 2020

Notes from our professors 3rd vector video. Also, homework 1 has been supplied! Do that asap.

Notes

There is a one-to-one correspondence between the free vectors in 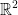and the points P(a, b) of .

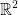Say we had the points A and P, we have the following:

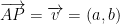
From now on, any vector will be considered as having start point (0, 0) and end point (a, b).
So then, 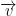= (3, -1) we mean a ray that goes from (0, 0) to (3, -1).
Also, vectors are usually bolded in the books but on paper we can use the right arrow above it.

= (1, -3, 5, 6)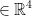

Even the number line is a vector space!

For a vector space, we have 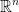, addition, and scalar multiplication.

In 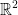consider the vector 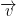= (a, b) and 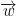= (c, d).
Find .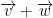
We have: (a + c, b + d)

Scalar multiplication extends the vector in the same direction (unless negative then it flips).
3(a, b) = (3a, 3b) = 3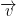

Definition: Let V be a set equipped with two operations. Addition and scalar multiplication such that:

1. Associative
2. Commutative
3. There is a neutral element 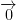. This is a 0 vector.
4. For each element 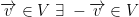(The backwards E means 'there exists') such that

The above are all axioms for addition!

Scalar multiplication:

1. Associative
2. Distributive for example:
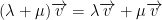   1. (that's lambda and mu)
3. 1 *
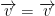
4. -1 *

The above are all axioms for scalar multiplication!

Then we say that V equipped with addition and scalar multiplication is a vector space!

HW

For the HW, he will be asking if we have a vector space. To be a vector space as he describes each problem, they must satisfy the above axioms! Otherwise, we do not have a vector space.

Solutions will be sent Monday before 10am so we can take a look before the lecture starts.

Subspaces (This is very important for the homework)

Normally when we have a vector space, we also have a subspace.
Let V be a (real) vector space and let W V (let W be a subset of V).
We say that W is a vector subspace of V if W is a vector space under the same operations as V.
In V, we can take any two elements and add them. Now, if we take any two elements in W then we should be able to do the same thing. HOWEVER! If we add two elements in W but get something in V then it is not a vector subspace! It only works if the addition remains within this subspace. The same goes for scalar multiplication.

More definitions:
Let 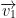and 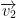be two vectors in vector space V or (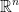) we say that 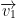and 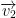are linearly independent if and only if 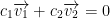then c₁ = c₂ = 0 .

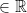Once again: Our vectors are linearly independent if the only way to add them to a zero vector is if all of they scalar coefficients are also 0!

Counter example: any vector that is not a zero vector,
then {} are not linearly independent. Why? because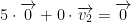
This contradicts c₁ = c₂ = 0 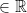for c₁ and c₂ don't both have to be 0.
This counter-example is a good way to check whether or not two vectors are linearly independent.
We can generalize all of this by saying 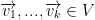(or 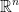) these are linearly independent if and only if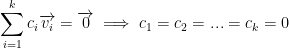

More on Linear Independence

I found myself a tad bit confused on what it means to be linearly independent vs linearly dependent. As such, I did a little more research on my own.
Once explanation I found is that vectors which are linearly independent represent directions in your vector space. Linearly dependent vectors on the other hand do not represent directions in your vector space.

For visualizing what this means (in ones head at least), I like this excerpt from Wikipedia:

"A geographic example may help to clarify the concept of linear independence. A person describing the location of a certain place might say, "It is 3 miles north and 4 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude and the curvature of the Earth's surface). The person might add, "The place is 5 miles northeast of here." Although this last statement is true, it is not necessary.

In this example the "3 miles north" vector and the "4 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "5 miles northeast" vector is a linear combination of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary.

Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe all locations in n-dimensional space."