Vectors Pt. 1

Created Tuesday 02 June 2020

PDF Notes

Vectors

Scalar quantities only have a magnitude. By this, they have a size but no direction. Mass and temperature are examples of such quantities for they both have some value but no direction.

A vector on the other hand is like a scalar in that it is a line segment with magnitude but also direction! An arrow is used to specify the direction. For example, 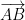has the initial point A and the terminal point B. The magnitude (or length) of the vector is the length of the segment AB and is denoted by .

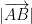Two vectors are equal if they have the same magnitude and direction.

Vector Addition

Vector 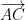is the sum of vectors and 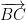when it is the displacement of u = 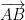followed by the displacement of v = .

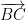Vector Multiplication by a Scalar

If a is a real number and v is a vector, then av is a vector of magnitude |a||v| and has the same direction as v if a > 0 or the opposite direction as v if a < 0.

Vector Difference

The difference of two vectors u and v is defined by u - v = u + (-v).

In the coordinate plane, a vector v can be represented as an ordered pair of real numbers, 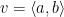, where a is the horizontal component of v and b is the vertical component of v.

Component Form of a Vector

If a vector v is represented in the plan with initial point P(x₁, y₁) and terminal point Q(x₂, y₂), then .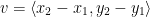

Two vectors are equal iff their corresponding components are equal.

The magnitude or length of a vector 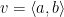is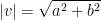

Algebraic Operations on Vectors

If 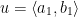and 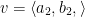, then we can do the following:

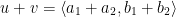
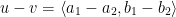
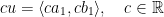
Properties of Vectors

Vector Addition

u + v = v + u
u + (v + w) = (u + v) + w
u + 0 = u
u + (-u) = 0

Length of a Vector

|cu| = |c| |u|

Multiplication by a Scalar

c(u + v) = cu + cv
(c + d)u = cu + du
(cd)u = c(du) = d(cu)
1u = u
0u = 0
c0 = 0

Vectors in Terms of I and j

The vector 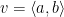can be expressed in terms of i and j by .

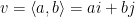Horizontal and Vertical Components of a Vector

Let v be a vector with magnitude |v| and direction 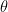. Then 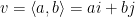, where

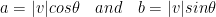
We can express v as .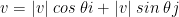

Examples

The rest of the pdf consists of example questions. The problems look to be very easy. Out of laziness, I won't be including the questions.

Also, here are some worksheets:
Addition
Subtraction

Video Notes

He introduces the idea of vectors_.

Before going into vectors, he will be reviewing the number line.

Firstly, 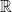= {x, x real number}. You can read this as, "R is the set of all real numbers."

On the number line itself, we have the origin which is 0. We can then fill it out with other numbers as well such as 1, 2, 3, 4, and so on. We also have a sense of direction that comes with this as well. To the right of 0, we have positive numbers. To the left, we have negative. Notice those words left and right. We have direction within this 1-dimensional line of real numbers.

2d Space

We can expand upon to the 2nd dimenional euclidian plane! I.e., the 2-d grid we've all become accustomed to. We represent all real numbers within this 2-d plane as 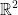. Notice that we square this!

On our 2-d coordinate plane, we can have any point P that is represented by an ordered pair of 2 real numbers. P = (x, y).
The origin is at (0, 0) of course.

The 2-d plane consists of 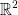= {(x, y), x, y }.
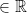Once again, the (x, y) are an ordered pair.

In regards to equality, (a, b) = (c, d) if a = c and b = d.

3D Space

Next, we have the space that of which we live in: 3 dimensional space! It consists of the following:
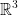= {(x, y, z) where x, y, z }
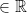The origin is of course (0, 0, 0).

Recap

So then, we have the following:

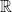A straight line that of which is the real number line. It consists of a single real number.
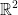A plane that consists of a pair of real numbers. (x, y).
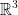Space corresponds to triplets of real numbers. (x, y, z).

These are all one-to-one.

Notice that we have a real space of n-dimensions (we'll be going deeper into this throughout the week).
We have the following: 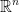= {(a₁, a₂, a₃, ..., a_n) where a_i 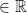for all i = 1, ..., n}

As you can imagine, we can also do this with complex numbers. We won't be doing this now but note that the complex numbers are much more useful in physics than with real numbers. Of course, it does get a bit more complicated.

As you may have infered, we can have this:
= {(x, y, z, t) where x, y, z, t }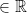
t is time by the way.

Vector Operations

There are various operations that we can perform in 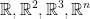space.

Firstly, let us go over addition.
Definition:
(a₁, ..., a_n)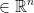
(b₁, ..., b_n)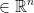

Add the corresponding components. Easy!
(a₁, ..., a_n) + (b₁, ..., b_n) = (a₁ + b₁, a₂ + b₂, ..., a_n + b_n)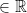

Next, he goes over the properties of addition of real numbers. Nothing new we haven't seen before.
(a + b) + c = a + (b + c) associative property
a + b = b + a commutative property
If exists a unique real number 0 (zero), then a + 0 = a. The property of zero.
If a is a real number, then (-a) such that a + (-a) = 0. Additive inverse property. (Or, the negative).

These properties we just went over satisfy the vector addition we did above.