Extrema Lagrange Mult

Created Monday 29 June 2020

We just finished with tangent stuff back in lecture Derivatives:Chain Rule - Tangent Plane.
Now we do other stuff before moving onto integration in the following week.

Let's Begin

A hypersurface is one in which has more than 3 dimensions. Also known as the level surface.

We learned that if we do the following:

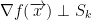
Then we get a vector perpendicular to the surface S_k at point x.

We have these two equations on that note:

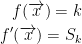
These help us to find the equation for the tangent plane.

Consider the tangent plane to the surface S_k at the point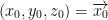
We have this equation which is the equation for the tangent plane:

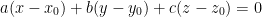
Where the coefficients (a, b, c) is a vector perpendicular to the tangent plane at x₀.

But!
Is what we call n. The normal vector.
However!
a, b, and c are the following partials:

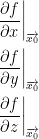
Each one can be read in the format of, "the partial relative to x (or y or z) at x₀."

Putting this all together, we have this expanded equation for the tangent plane:

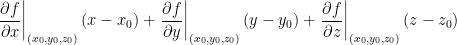
Example

Find the equation of the tangent plane to the surface z = 4x³y² + 2y at the point (1, -2, 12).
He goes on at the 10:04 mark to rewrite z as the following function:

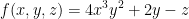
As such, all points that satisfy this equation equal 0.

First things first, we need the gradient. Remember, that gradient is just a vector consisting of the partial derivatives like so:

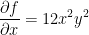
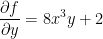
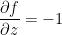
at the point (1, -2, 12) we have the following:
For simplicity, point p = (1, -2, 12). Okay now we have the following:

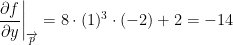
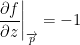
So, all we had to do we plug in the numbers from our point (1, -2, 12) into our partial derivatives.

Continuing on, the equation of the plane is as follows:

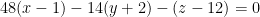
We can then simplify like so for our final equation:

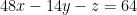
In case you didn't make the connection, remember that this is the equation for the tangent plane:

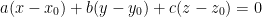
Critical Points

Next, we shall cover, as our professor writes, the following:
CRITICAL POINTS of a function

Soon, we will cover maxima and minima so we will need to know this. This will be on quiz 2 by the way! I believe so anyways.

Let's begin.

Let us have an open set 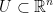such that:

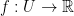
Definition

We say that the point 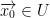is a local minimum of f iff there is a neighborhood we shall refer to as 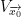(which can be read as, "V of the point x₀") such that:

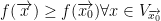
So, it's just a bunch of points really close to our x₀ from my understanding.

Anyways...

x₀ is a critical maximum if we have the opposite like so:

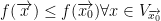
Another Definition

We say that the point 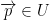is an extremum of the function iff p is a local maximum or a local minimum.

So, an extremum is either max or min point. That's it. That's what it is.

Def: We say that 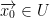is a critical point for the function f if f is differentiable at x₀ and if:

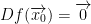
One Last Definition

A critical point which is not a local maximum or a local minimum is called a saddle point.

Theorem

Remember, U is a open set in . Moving on...
If 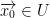and f is differentiable and x₀ is a local extremum (which means it is either a local max or local min) then:

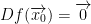
In other words, x₀ is a critical point.

He says that we should know from calculus one that if a point is a maximum or a minimum then its derivative is 0!

Proof

Assume that x₀ is a local maximum (or local minimum. Doesn't matter).
Then, 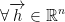the function (which is a real function of one variable):

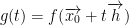
Then the previous equation has a local maximum at t = 0. Why? Because th becomes 0. Then we just have f(x₀). Then by assumption, f(x₀) must be a maximum of g(t).

From calculus 1, we know that for this to happen the derivative of the function g is 0 like so:

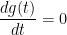
By applying the chain rule, we know that:

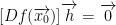
Please note! In general, h is not 0. As such, the derivative Df(x₀) must be 0.

Example

Find the critical points of .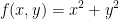

First off, we have the following derivatives:

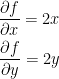
Now then, for us to have a critical point the derivative must be 0 for both partials at the same time. As you may be able to tell, this only happens at the point (0, 0).

As such, the only critical point is the point (0, 0).

By taking a glance at our function f(x, y) = x² + y², we see that (0, 0) must be a minimum. Why? Because our function only produces values bigger than 0 except when both x and y are 0.

Two Definitions

We say that the point p = (a, b) is a saddle point for a function f if in one direction you have p as local minimum and in another direction you have as local maximum.

Now the other definition (he says that for the following, if we go beyond 2 dimensions then the definition will need to change a little. Just keep that i mind).

If we have the function 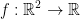we call the Hessian of f at the point p is the following Hessian matrix (H stands for, "the Hessian" by the way):

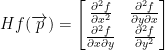
If the function is differentiable, then the top-right and bottom-left elements of the Hessian matrix are equal.
Also, the above equation is referred to as the Hessian.

Also, it has a determinant. Which makes sense considering it's square-ish shape.
If you already forgot what a determinant is, refer to Matrices:Dot Cross Prod for more information.
Anyways, here's wonder wall the determinant:

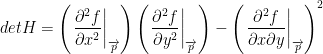
If you're wondering why we squared that last bit in the equation, it's because the bottom-left and top-right portions of our Hessian matrix are equal if the function is differentiable. So, we can just square it.

A Theorem (Without Proof)

He says the proof is super complicated so we won't go over it. Anyways...

Let 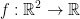. If the derivative of your function at a given point is 0, then:
1) If the determinate Hessian of f is positive, then we have the following:

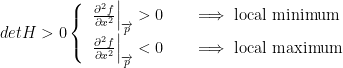
2) If the determinate Hessian of f is negative, then we have the following:

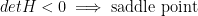
He also makes a quick note about how x₀ = p.

3) If the determinate of the Hessian of f is zero, then we have nothing to conclude. We got no idea what do here.

Example

Find the critical points of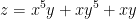

First, find the partials relative to x and y.

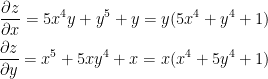
Remember, for us to have a critical point we need the derivative to be 0. As such, the previous two partials need an x and y value that makes them become 0. We quickly see that (0, 0) does this because:

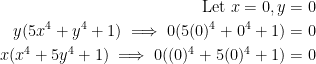
As such, our critical point is (0, 0).

Next, what kind of critical point do we have? A max or min? To solve this, we must find the second derivative like so:

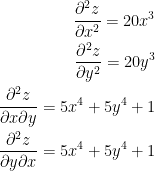
Notice how the mixed partials give us the same result.

Now then, we can plug this all into a Hessian matrix like so:

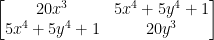
Plugging in (0, 0), we have:

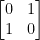
Finding the determinate of that, we have -1 because 0*0 -1*1 = -1

Because the determinate of our Hessian is -1, we have a saddle point. Why is it a saddle point? Because:

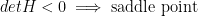
Lagrange Multipliers

The final topic of this lecture.

Lagrange multipliers is about constraining the maximum and the minimum. It's all about optimization.

Theorem

If and 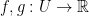with continuous derivatives.

Assume that 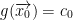and take the surface and assume that 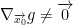. Then, there is restriction (which means we only plug in points to f that belong to our surface) of f on 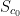has an extreme value at:

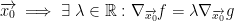
Okay, now for an example. He says that if we know one example then we know everything. It's all very similar. I'll take your word for it professor...

Example

Optimize 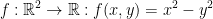given that x² + y² = 1.

So basically, we want to know if our function f has a maximum or minimum when we only plug in points from x² + y² = 1 (which is the unit circle by the way).

Solution

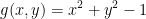
So then, when g(x, y) becomes 0 we get x² + y² = 1.

Moving forward, we have:

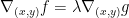
Taking the derivative of both f and g, we have:

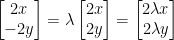
So, remember that g(x, y) = x² + y² - 1 and f(x, y) = x² - y².
As such, to get the matrices of their derivatives equal to each other we can do the following:

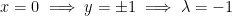
or

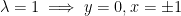
Why the plus/minus for y or x? It's because we want x² + y² - 1 to be 0.

Bringing this all together, our potential critical points are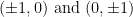

Now then, if

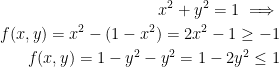
This shows that the points (1, 0) and (-1, 0) are maxima. Also, points (0, 1) and (0, -1) are minima.