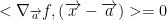Chain Rule - Tangent Plane

Created Thursday 25 June 2020

To begin, remember that the derivative is a linear function between two spaces.
Not only that, a linear function has a matrix that represents it that of which is mxn.

And of course, we have the Jacobian matrix like so:

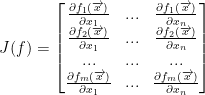
Properties of the Derivative

1)
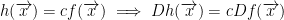
Which essentially just means we can pull out the constant in a linear map.

2)
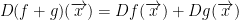
This is because they are linear functions that we can do this.

3) Chain Rule
This is just like the chain rule back in calculus 1.
In case you forgot what that was, observe:

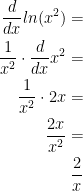
This was my own example and not his.

His example of the chain rule is this:

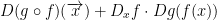
Special Case

Let m = 1 so we have the following: 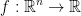. Notice I didn't write m on the second R. This is because it is 1 so we don't need to write anything.

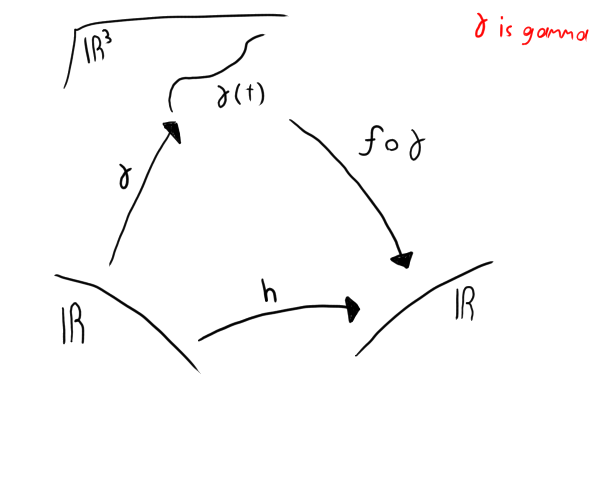
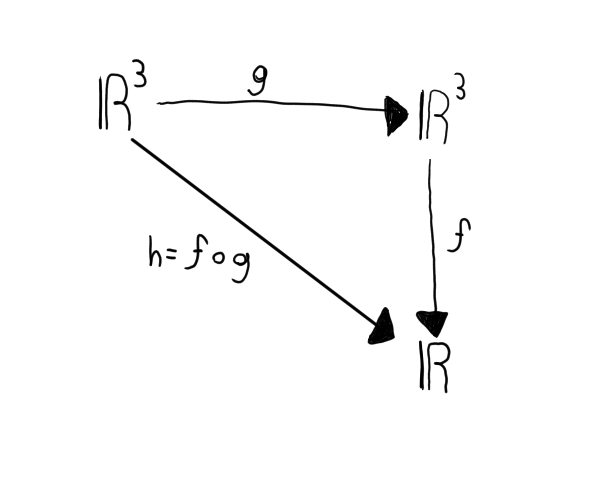
Consider the following (γ is gamma and we are using it as a function by the way):

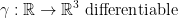
Also, the 3 is being used in place of n to make things easier to understand. So then, γ is going from our 2nd space to our first space.

Here is a diagram to illustrate a bit about what is occuring:

We also have the following:

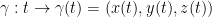
And also this:

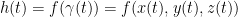
And here is a derivative:

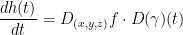
In turn, the 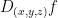will give us a 1x3 matrix as follows:

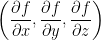
And:

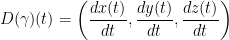
Putting this together, we get the following which is an inner (dot) product between two vectors.:

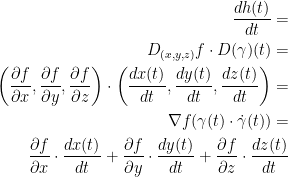
It might be hard to tell, but the very last 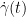in the above equation has a dot above γ. This means the derivative of gamma.
Also, remember that ∇ is known as nabla. Refer to Jacobian Derivative to learn about what this does.

Proof of the Chain Rule

He prewrote this portion of the video. Needless to say, it will but quite the gauntlet to decipher everything he wrote...

Let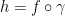
Then:

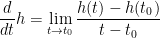
But! We also have this:

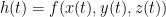
So then, we now have this hot mess:

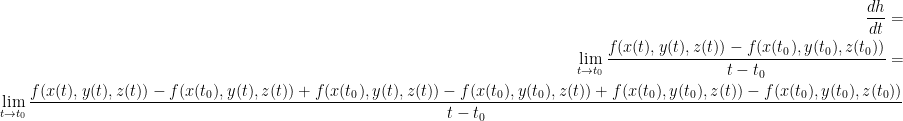
If you look closely, though, you'll see in that final monstrosity of a fraction a lot of this stuff actually cancels out!
Also good to note that each one of the above he says is a partial derivative. At least, for the last fraction.

He wrote a little bit more after this but I couldn't quite tell what it was. We should inquire about him sending us a photo of his proof of the chain rule. Nonetheless, I don't think it's too important. He's merely proving the chain rule which we should all have ingrained within us already.

He has another paper with a bunch of matrices that he uses to further prove the chain rule. He essentially just says that we take the Jacobian of f and multiply it by the Jacobian of g.

He gives us this formula but I am unsure if it is correct. I could hardly see it! This is the best I could make out so double check it:

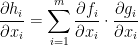
Examples

Oh no... He prewrote these as well!

Example 1

Verify the chain rule in the following example:

Where we have the following:

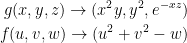
This in turn gives us:

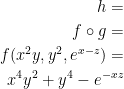
This implies that the partial derivative of h in regards to x is as follows:

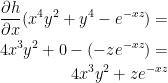
Also, based on what we were studying earlier in the lecture we have:

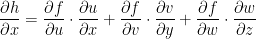
He writes out the details of calculating this but I can't really see it. It's essentially just the long way to get the same answer we got above. Which was:

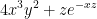
In case you already forgot.

Example 2

This problem isn't so bad. We just want to find 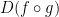at (1, 1).

Imagine a triangle that looks like this:

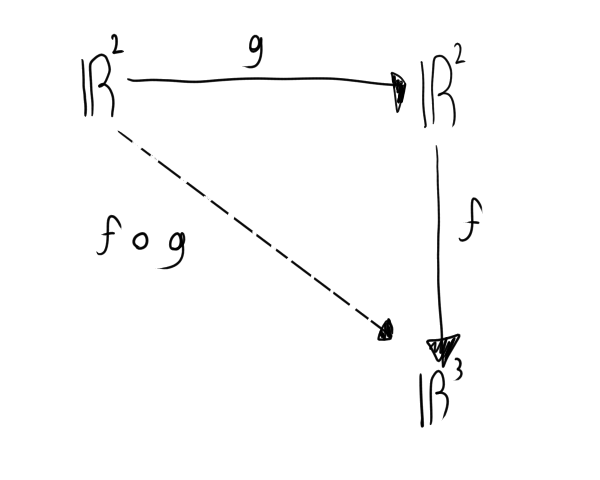
Let our functions be defined as:

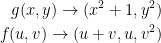
To begin, we need to find the Jacobian matrix for both functions.
Starting with function g, we have the following:
Let:

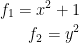
Then:

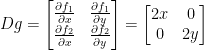
Now for function f:
Let:

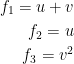
Then:

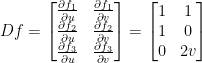
Great! So we have the Jacobian matrices for both f and g. But now we wanna find 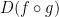at (1, 1).

First off, let's plug this into our Jacobian matrix for g like so:

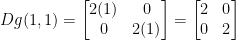
We also have this: g(1, 1) = (1² + 1, 1²) = (2, 1).
Since we are going from g to f, let's plug (2, 1) into f like so:

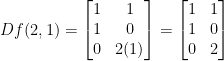
Fantastic! We're almost done. Now we can just multiply these matrices and get our final answer!

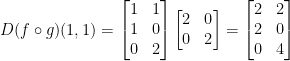
Now for something important (again)

Consider the case m = 1. This means that our function .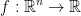
This implies the following:

By the way, this is read as, "the derivative at point a..." in case you weren't sure why it was written like that.

Anyways...
There is a theorem which states that if:
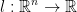is a linear function, then we can find a vector .
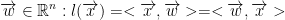We can find the inner (dot) product like this so long as w is a constant vector in 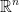space.
He also notes that: w depends on l (which is a lowercase l).

Moving forward, w is also known as the gradient of f at point a. We write that like so:

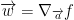
We also have this important equation:

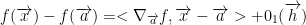
And now for another important theorem!
Let u be a direction vector. We have this theorem:

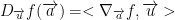
To get the above theorem, you apply from the equation above it the following:

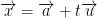
Prove the Following

Let 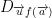be the directional derivative of f at the point a in the direction u. As such, we have:
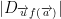is the maximum value when the direction u is .

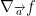He states that the proof is easy.

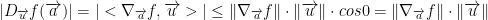
Do not forget the formula for the inner (dot) product! It is as follows:

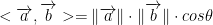
Also, do not forget that cos(0) = 1. As such, if the angle between is the vectors is 0 then they are parallel.

Remark:

So, let's observe the following partial dertivative. Remember, e_i is the canonical direction. I.e., the natural basis directions! You know, (1, 0, 0), (0, 1, 0), and (0, 0, 1) for the third dimension. I hope you remember this... Anyways, here it is:

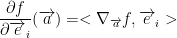
As you can probably tell, it's similar to what we were working with before but instead of the direction vector u we're using the canonical directions of e.

Curves

Now we talk a little bit about curves.
Let be a differentiable curve. Also, γ is known as gamma in case you forgot.
So then, let us take the derivative of gamma like so:

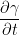
He says that the derivative of γ is the, "derivative of each component." I would write what those components were but I cannot see them for the life of me.
Anyways, in simple terms the derivative of γ gives us the velocity. Not only that, it is the tangent line to at the point t. The second derivative gives us acceleration.

Another important theorem

Another very hard to read thing...

Let 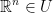which is an open set.
We also have 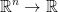which is a differentiable function.

The level set c of f is a set as follows:

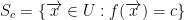
For example, the sphere.

The level will be a sphere 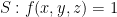where 1 is the radius of the sphere.

The set S_c is known as the hyper surface in 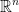and has the dimension m = 1.

Now for another theorem

If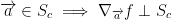
I.e., if v is the tangent vector at t = 0 of the curve 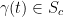with 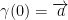then we have the following:

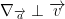
Proof

Please note, I did the best I could to copy what he wrote. Some of this might not be accurate though...
Let 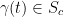with 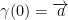. Then the tangent of a will be the derivative of your function when t = 0 and .

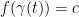In other words, f is a constant function in t.
Applying the chain rule, we say:

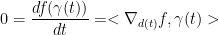
and for t = 0 we have

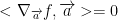
So the tangent vector at a of all curves passing through a from a plane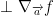

This is called the tangent hyperplane to the surface S_c at a and its equation is (I don't know if this is right. Once again, could hardly tell what he wrote. Here's my best crack at it nonetheless):