Lines and Planes

Created Monday 15 June 2020

Today we will focus on lines and planes in .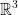

We want to find the equation of the line passing through the point a = (a₁, a₂, a₃) and having direction v. In other words, it is parallel to vector v.

This also implies that our point must be on a line that is parallel to our vector v. This other line will be of some multiple of vector v. We can write this as tv.

Say that we also have vector a that is orthogonal to v.

We have the parametric equation:

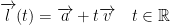
Let 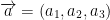and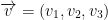

With this, we now have:

Our line is the set

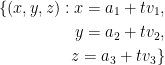
Remember, : reads as, "such that..."

From that, we get this parametric form of our equation:

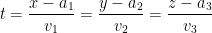
Example:

Find the equation of the line where a = (1, 0, 2) that is parallel to v = (-1, 2, 3).

So then, we get this:

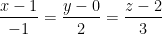
Planes

A plane is defined by a point (a, b, c) and two vectors (i.e. two directions) like so:

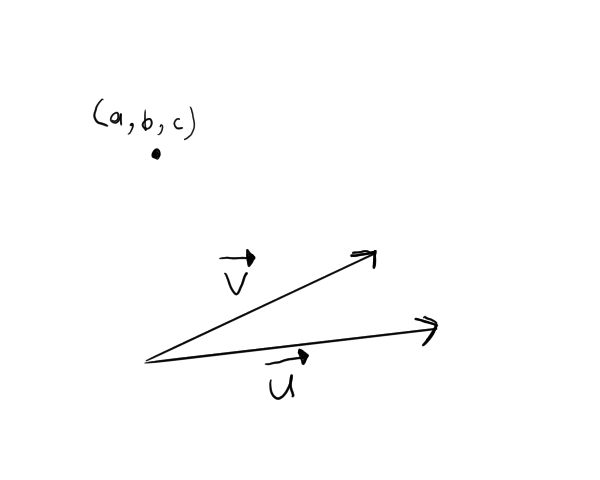
So, we have this:

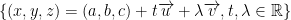
Alternative Definition:


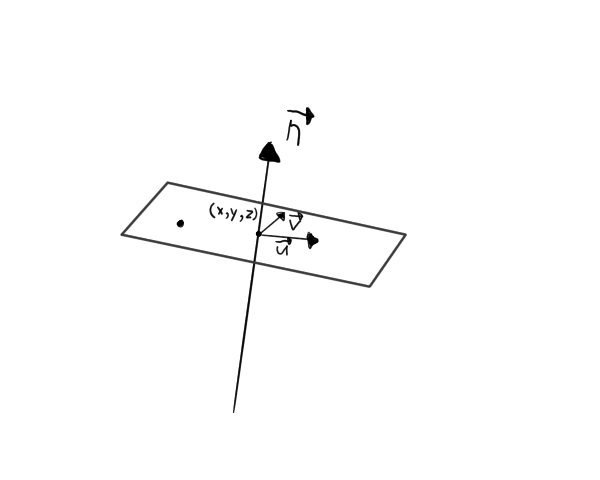
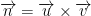
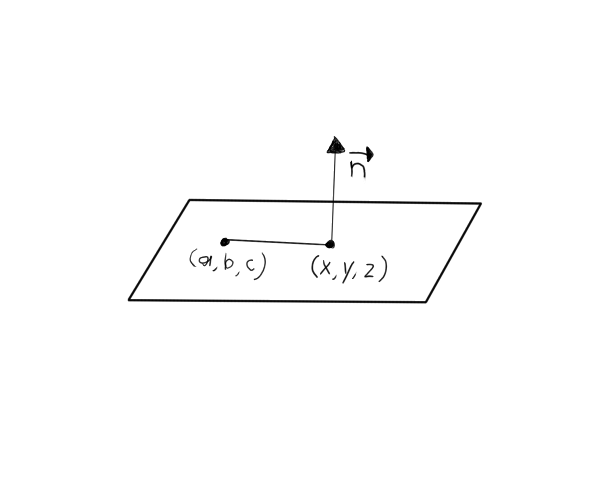
We have a point on the plane defined by the vectors v and u. Vector n is the cross-product of these two vectors.
So our plane is determined by a point (a, b, c) of the plane and a vector n which is perpendicular to the plane.

In other words, the dot (inner) product with any point passing through n must be zero.

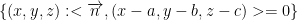
So then, we take our point (a, b, c) and try to center it on to n. Then, if the result of the dot product is 0 all is well!

Examples

To reiterate, we're trying to see if we have a point perpendicular to vector n.

Remember: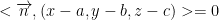
Now then, let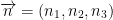

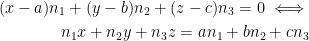
Let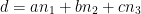

We now have the equation for the plane:

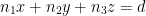
or we can write:

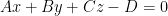
which is the equation for the plane which is perpendicular to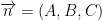

Quiz

He said we'll have a question about the line and the plane on our quiz on wednesday!

Exercise 1

Find the equation of the line containing the points (1, -1, 2) and (2, 1, 0).

Solution

Immediately, we have a vector v = (2, 1, 0) - (1, -1, 2) = (1, 2, -2).
What this really gives us though is the direction of the line!

The equation of the line is:

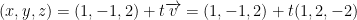
To get t, we do this:

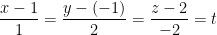
Exercise 2

Find the equation of the plane containing the point (1, 0, -1) and the line given by x = 2 + t, y = -4t, z = 2+t

Solution

Firstly, the coefficients of t make up the direction vector!
In this case, we have (1, -4, 1).
Now, we need another direction of the plane. To do this, we need any point on the given equation of the line. To do this, simply replace t with any number. The easiest would be 0 of course.
This gives us the point (2, 0, 2).

Now then, let us get another vector w like so:

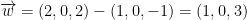
As such, w is our other direction.

Now then, we have this:

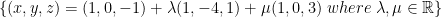
More on Quiz

This is it for the first quiz. You only need to know everything up to here.
ifarmakis@brooklyn.cuny.edu is where we email to up to 10:35am. Remember, we have an extra 5 minutes to send in the exam. Don't cheat he says or you get a 0 for everything.

If you don't send on time, he won't take the exam into consideration which is the equivalent of a 0.