Homework 3

Question 1

Show that every linear map from a one-dimensional vector space to itself is multiplication by some scalar.

My Answer
I'm not 100% sure what is being asked but here is my attempt:
Let , ,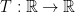

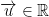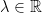
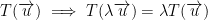
Therefore, we see that every linear map from a one-dimensional vector space to itself is a multiplication by some scalar due to λ.

In addition, I also have this example:

As such, when we multiply vectors a and b together, we get the following:

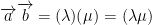
Likewise, we get the same result when multiplying by the scalar versions of each vector like so:

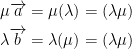
Therefore, we can see that multiplication between 1-dimensional vectors is the same as multiplying them by a scalar.

Professors Answer
My reasoning is similar to that of the professor's. I'm running low on time so I'm not gonna discuss it. I'd copy and paste but it's got symbols n' stuff I can't copy :\

Question 2

Give an example of a function 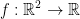such that for all 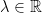and all 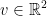but f is not linear.

My Answer
To be a linear map, it must be able to do the following:

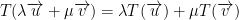
In our case, f works with scalars such that .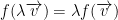

To give an example of a function f that is not linear, let us have the following:

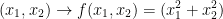
Let us find a matrix A that corresponds to our function f. To do this, let us use the basis vectors for R².

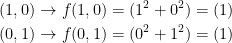
This gives us the matrix:

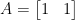
Which implies the following:

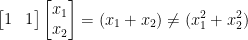
3) Define the map .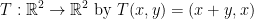

1. Show that T is linear.

My Solution:
To show that it's linear, we must see if addition and scalar multiplication holds like so:

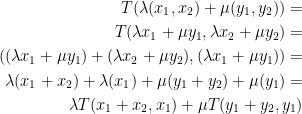
As you can (hopefully) see, it all holds!

2. Show that T is surjective

I don't believe we ever went over this term. I'll try to answer anyways.
A quick search online reveals the following definition: Suppose 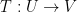is a linear transformation. Then T is surjective if for every 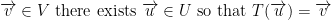. From what I understand, that means from every possible u there should be a corresponding r after applying the transformation (aka, we run it through the T function).

I can up with the following proof. I'm not sure if it's correct but here we go anyways:

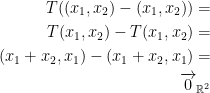
Question 3

Question 3 Pt. 1

My Answer
Find the matrix for T with respect to the canonical basis of R²
Oh! I think I got this one! We're just finding the matrix that goes along with the linear map. Let's begin!
First, we have the basis vectors ( 1, 0) and (0, 1). With those, we have the following:

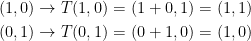
Great!, so the resulting vectors make up each column of our matrix! Observe:

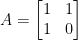
And that's it! We can double check our work like so:

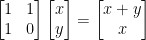
Wow! Just like we saw earlier! Hurray.

Also, here is another way:

Question 3 Pt. 2

Question 3 Pt. 3

Question 3 Pt. 4

Show that the map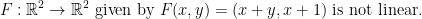
Here, we just do what we did in part 1 of the question. However, we'll soon see that the '+ 1' portion of the function gives us trouble!

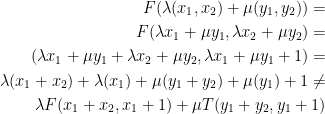
As you can hopefully tell, we end up with a single lingering +1. However, that is not enough! We need two +1's if anything to make this all work. Plus, we can't distribute the λ or μ over the +1 without just changing it to λ or μ. As such, scalar multiplication and addition do not hold! Therefore, we do not have a linear map/function.

Professor's Answer
He told us to just solve it on our own... Thanks I guess...

Question 4

Let M_2x2 be the vector space for all 2 x 2 matrices with entries the real numbers, and let B be a fixed 2 x 2 matrix. If we define the map 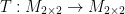by:

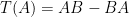
verify that T is a linear function.

The following is my best attempt. I spent way too much time on this.

Question 5 pt. 1

Another question in which the professor tells us to solve it on our own...

My Solution
Well, these seem easy enough. We just need to turn the linear transformation into a matrix. Observe:

Let 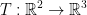defined by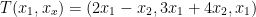

First, let's give the function T the basis vectors (1, 0) and (0, 1) as input like so:

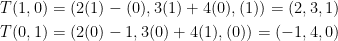
Great! Each basis vector forms a column in the final matrix like so:

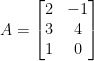
where A is the matrix representing T.

If in doubt, you can multiply it out with the input. If everything lines up, we gucci!

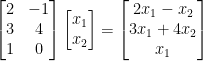
Oh hey! It matches. We are complete!

Question 5 pt. 2

My Solution
Same thing as in part 1. Let's get crackin...
Let 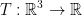defined by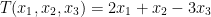

Once again, we plug in our natural basis vectors:

Each one forms a column like so:

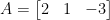
And tada! We are done. Once again, we can check like this:

Question 6 pt. 1

My Solution
Not bad! Just multiply the given matrix by the vector (1, 0, -1, 3, 0) like so:

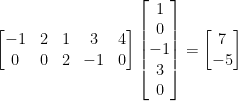
As such, our final answer is (7, -5). Hopefully the multiplication is easy enough that you can see how I got that.

Professor's Solution
Oh my lord there is an answer...
It's (7, -5)

Question 6 pt. 2

My Solution
:\ The professor didn't teach us how to do this at all. Here is my attempt after doing some research on the subject:

I'm using a method known as Gaussian elmination. It consists of the following steps:

1. Convert system to matrix-ve ctor equation
2. Augment the coefficients matrix with the vector of constants
3. Use Gaussian elimination to create a matrix with 1's on diagonals
4. Map the matrix back to the equations
5. Back-substitution to solve for variables
6. Check your work using the original system!

All of this information I obtained from a course on Udemy for linear algebra.

Fuck. I wrote out everything and lost the file cause I resized krita to be too big and forgot to save.

Well, using my solution I got this as the pre-image:

Multiplying it out, you'll see that it works like so:

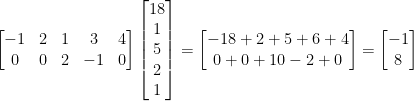
And what do ya know, we were looking for the pre-image of (-1, 8). We did it!

Professor's Answer
(1, -11/2, 5, 2, 0)
Both my answer and his work. The hard part is just finding what combination of numbers work. I am deeply sorry that I couldn't provide my detailed notes on how I got my answer. Look up Gaussian Elimination online and try to follow along with whatever tutorials you find.

Question 7

My Solution
Not gonna lie, I have no idea how to approach this one right from looking at it. Thankfully, our professor gave an answer that I will take a moment to explore.

Professor's Solution
So, we have this matrix:

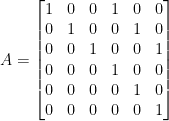
We are then asked to find a formula for A^k for any positive integer power k.

Now then, looking carefully we see that there is some sort of pattern occuring with this matrix. Take a look at each 3x3 corner of the matrix A. We see that we get:

For the top-left, top-right, and bottom-right corners. These are all identity matrices that we shall denote as I.
In the bottom-left corner, we have nothing but zeroes. As such, it is the 0 matrix.

As such, we see we following:

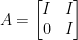
Taking A to the second power, we get this (our professor made a typo on the answer sheet. The top right corner should be I as I have written below):

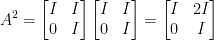
Then to the third power, we get this:

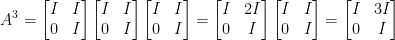
If you continue multiplying, you'll see this pattern:

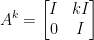
And that's our answer!

Question 8

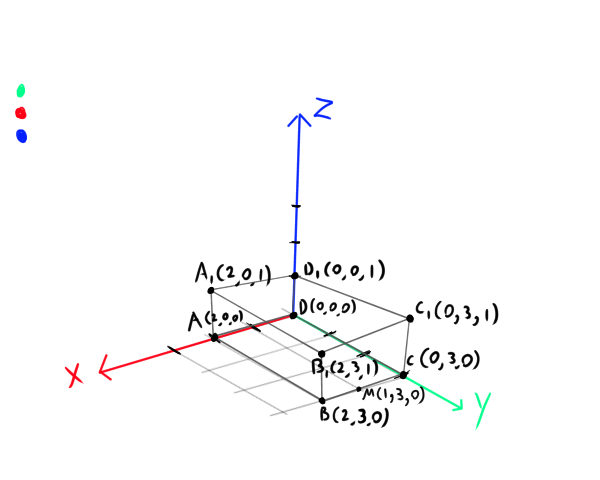
Question 8 pt. 1

Find the equation of the plane containing the points A, D₁, and M.

This one isn't so bad. First, let's note what our points are:

Next, we need to find an equation for our plane. To do so, we need to choose a starting point. The professor chose point A and I will do the same. So, we have the following two vectors from point A:

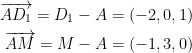
Awesome! So then, if you look closely at the diagram I drew above, you can visualize a sort of plane being formed by these two vectors. Now we need a vector that show's how the plane or oriented. This would essentially be our vector n back in the Lines and Planes lecture.

As you hopefully remember, the cross-product gives us a vector orthogonal to two other vectors. Check it out:

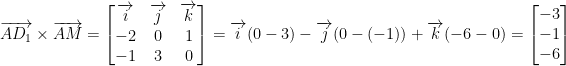
Almost done! To get the equation of a plane we do the following:
Let n = (-3, -1, -6) and a = (2, 0, 0) which was our point A from earlier.
We now find the dot product and set it equal to 0 like so:

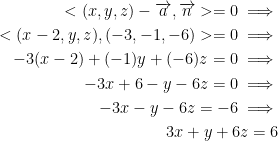
And so, the final answer is:
3x + y + 6z = 6

Question 8 pt. 2

Find the area of the triangle A D₁ M.
Remember, we have the following points:

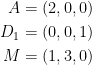
Now then, remember the law of parallelograms and that by finding the determinant we get the volume between two vectors. How do we find the determinant? By finding their cross-product! Note, this cross-product gives you the volume of the parallelogram formed by the two vectors when we find it's magnitude. Not only that, a parallelogram is just a sort of rectangle. If you think about it, a triangle is just half of a rectangle. So, where am I getting with all of this?

I'll show you!

First, we need a starting point that our two vectors are protruding from. Let's make it A again. That way, we get the following:

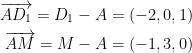
Next, we must find their cross-product like so:

Great, now let's find the length (or norm) of the cross-product:

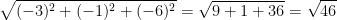
Yay! We now have the volume of the parallelogram formed by our two vectors. But a parallelogram is rectangular and we want a triangle...

Oh.

Just divide it by 2.

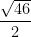
That's our answer!

Here is a shortcut:

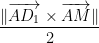
Question 8 pt. 3

Find the parametric equation of the line .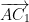

First, let us define the vector as follows:

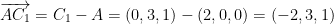
So then, that gives is the direction of the line.

In case you forgot, the parametric equation is as follows:

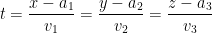
Where a is some point and v is a direction.

As for the actual equation of a line, it takes the form of:

Let a be (2, 0, 0) and v be (-2, 3, 1).

We get the following:

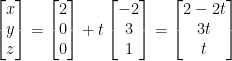
As such, our final solution is:
x = 2 - 2t
y = 3t
z = t

This is also the professor's solution.

Question 8 pt. 4

The professor doesn't give an answer for this one. I'm running low on time so I'll return to it later if possible.

Question 9

If A₁, A₂, ..., A_k are open sets in 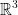show that:

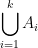
is an open set.

Personally, I really don't know how to do this. The professor's solution I am mystified by as well. Nonetheless, here is what he said:

Be this the case, then there must exist an open set A_j such that .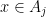
Now, since A_j is an open set in 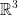, there must exist an open ball B_x(r) such that:

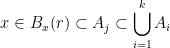
In B_x(r), x is the center point and r is the radius.

If it helps, think of the open ball as a sphere that our point is inside. It's an open ball because our point can be anywhere inside the ball but never on the edges. The same principle applies to an open set.

Also, every open ball is an open set as per this article.

Question 10

Looks like he doesn't give any explanation once again :\
Ah shit, here we go again.

My bad. He put it on the other solution pdf...

Question 10 pt. 1

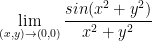
The answer is 1. I'm not completely sure what the 'correct' way to solve this is but here's my take:

Let y = 0. Then we get:

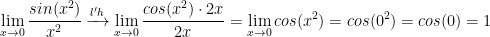
If you let x = 0, then you get the same result as above.

Since the limit is 1 for both x and y, the answer is 1.

Question 10 pt. 2

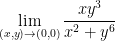
My attempted answer is 0.
Let x = 0.

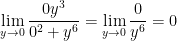
Great! Now let x = y.

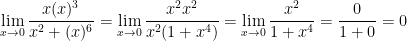
So, when y approaches 0 our limit is 0 and when x approaches 0 our limit is 0.

However! The professor states that a limit does not exist. If I had taken x = y³, then the limits would not match. I'm not completely sure why this is but, alas, I appear to be wrong.

Question 10 pt. 3

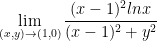
My attempted answer is 0. Here is my reasoning:
Let x = 1.

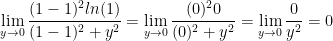
Let x = y

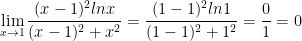
The professor takes a different approach and says that the limit may exist. If it does, then it's 0.

Question 10 pt. 4

To save time, I'm skipping this one. My attempt using the same method in the previous questions gave 0. The professor used polar coordinates to solve the problem and also got 0.

Question 11

Consider the following function:
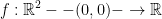given by

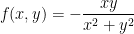
Find the limit along the following curves as

1) the x-axis
Let y = 0

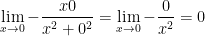
2) the y-axis
Let x = 0

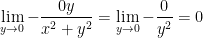
3) the line y = x

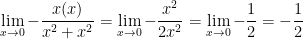
4) the line y = -x

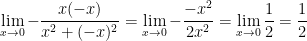
5) the parabola y = x²

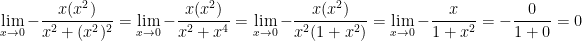
Question 12

Let 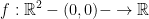be the function:

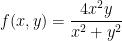
Use the definition of limits to show that

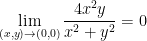
I'm not 100% sure of the reasoning behind the answer to this problem but this is what our professor wrote:

We want the following:

This happens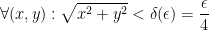
I'm getting sleepy. I'll see if I can come up with a better explanation later.