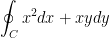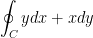Created Thursday 02 July 2020
Final stretch. Yay...
Question 1 a
Check if the following vector field is conservative or not:
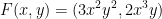
Let
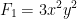
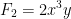
For us to have a conservative field, then we should have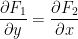 
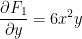
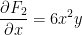
Since they are equal, F is a conservative vector field.
Question 1 b
If F is conservative, then find its potential function φ.
So, our potential function takes this form:
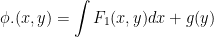
As such, when we integrate we get:
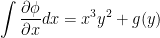
In turn, this implies the following:
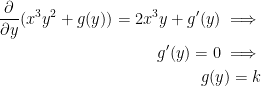
As such, we have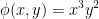 
Question 1 c
Evaluate:
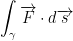
where γ is the line segment from (1, 2) to (4, -3).
To solve this one, remember that the fundamental theorem of calculus states:
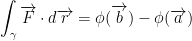
So, just plug in like so:
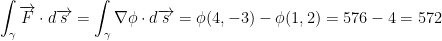
Question 2
Show that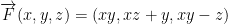 
is a conservative vector field and find a function φ such that 
.
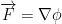I believe his answer is incorrect. Why?
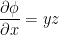
When it should be equal to xy.
Anyways, let's get this over with.
Let
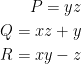
First, let's choose a variable to integrate with respect to. Let's do z.
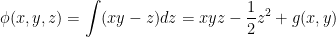
Next, we can differentiate this with respect to x and set it equal to P.
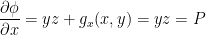
From this, we now have:
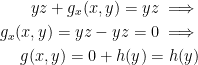
We now have this potential function:
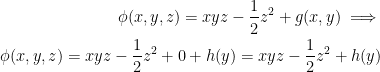
Finally, we need to differentiate with respect to y and set the result equal to Q like so:
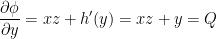
We now know that:
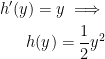
Putting it all together, we get:
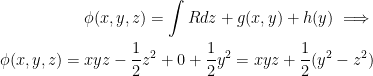
Yay! We did it!
Question 3
Let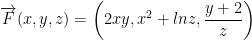 
. Show that F is a conservative vector field and find a potential function φ of F.
Same deal as the last question.
First, we have this:
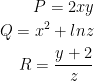
Next, let's choose a variable to integrate with respect to. Let's do z just like last time. It honestly doesn't matter but I'm used to it now.
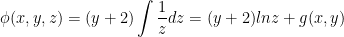
Next, we can differentiate this with respect to x and set it equal to P.
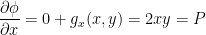
And now we have:
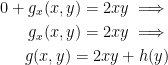
We now have this potential function:
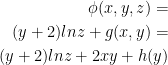
Cool.
Finally, we need to differentiate with respect to y and set the result equal to Q like so:
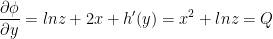
And now we have:
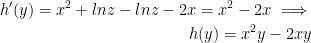
Last but not least, we have:
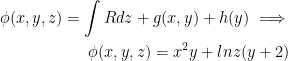
Yay we did it!
Question 4
Consider the vector field:
Determine whether F is conservative, and if it is, find a potential function for it.
This is quite the beefy problem but we solve it just as we did for questions 2 and 3.
Let's begin.
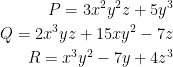
Next, let's choose a variable to integrate with respect to. Let's do z just like last time.
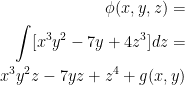
Now we need to figure out g(x, y). To do this, we can differentiate the integral with respect to x and set it equal to P.
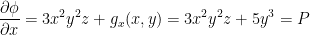
We then have:
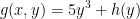
We now have this potential function:
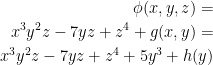
Finally, we need to differentiate with respect to y and set the result equal to Q like so:
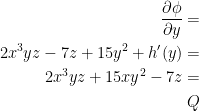
We then have:
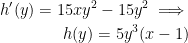
Putting it all together we have:
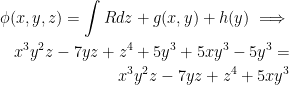
Holy shit I got it right!
I felt like I went terribly wrong somewhere but that's it. Same answer as the professor.
Question 5
Consider the vector field:
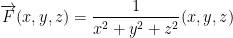
Is F conservative? If it is, find a potential for F.
I have no idea what F's politcal leanings are so let's just find that potential function.
Although we have the added bonus of one big annoying fraction, I'm assuming this should work just as everything else did.
Let's choose a variable to integrate with respect to. I will do z.
I'M GONNA SKIP THIS PROBLEM. The steps should be apparent now and I don't feel like integrating this devilish monster.
Question 6
Same problem as before.
Question 7
another one of the same problem
Question 8
Let F be the vector field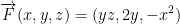 
. Evaluate 
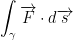, if γ is:
- the straight line segment from (0, 0, 0) to (1, 1, 1).
- the curve
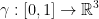such that 
.
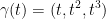First off, remember the fundamental theorem of calculus:
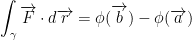
Also, for the first bullet point we know the following:
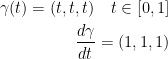
This gives us the following:
If you're wondering how we got (t2, 2t, -t2), this is how:
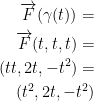
Now for the second bullet!
Remember, we have the following:
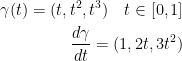
We then have the following:
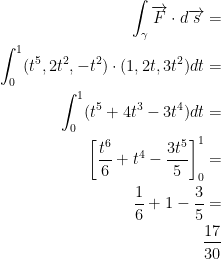
And we're done!
Question 9
Evaluate:
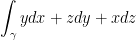
where γ is the ellipse formed by the intersection of the cylinder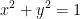 
and the plane 
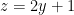oriented counterclockwise as viewed from above.
So then, this problem gave me anxiety. I wasn't sure how to approach it but I think I managed to figure it out.
First off, our vector field F is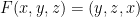 
. I assume this is based on how we integrate in the given integral.
Next, we parameterize the curve as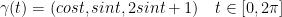 
.
How did we get this though? Well, our γ is an ellipse and it is formed by the intersection of the given cylinder and plane. We know that in polar coordinates we have a circle of radius 1 when we have 
. Likewise, we know that the plane has a z of 
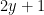. We know that y = sinθ so then we have 
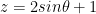. For our particular problem, replace θ with t and we gucci!
Next, we also know that:
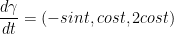
To make things a little more convenient, here is what we have all together thus far:
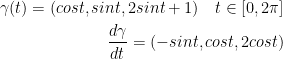
Great. Now let's solve this hoe!
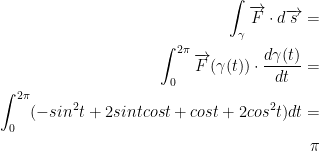
Sorry I skipped out on showing the integration. It was taking me a moment to figure out so I decided to just let an online calculator check that everything was in order. And it was!
The answer is π.
Question 10
Let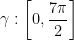 
be the curve 
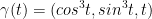. Evaluate the integral:
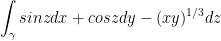
Once again, this formula is gonna help us out here:
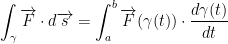
Let us have the following:
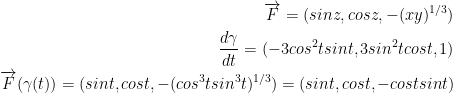
Let's crunch them numbers boi!!!
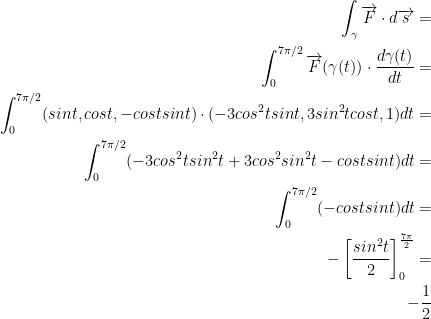
And that's it!
Question 11
Consider C to be the perimeter of the unit square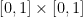 
in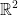 
, oriented in the counterclockwise sense. Evaluate the integrals:
Now then, the way to start this problem may not be obvious! That is okay. I had no idea either. Let's break down what is being said regarding the unit square first.
First off, each side of a unit square is 1 just like how a unit vector has a length of 1 or the unit circle has a radius of 1.
With that in mind, C is the perimeter of said unit square. If each side of the square is 1 then the perimeter is equal to: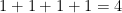 
.
Now, think of the perimeter of the unit square to be our closed curve γ. Therefore, γ has an interval of [0, 4].
With this information, we can assume the following:
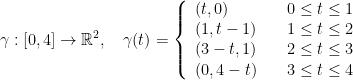
Now then, it took me a moment to understand the professor's answer for the first integral. Which was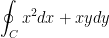 
in case you've already forgotten. After some trial and error, I finally got it figured out!
As in the last question, we're gonna need this formula:
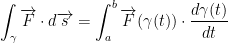
Let us have the following:
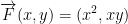
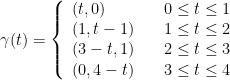
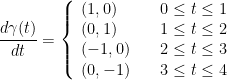
Now then, to achieve our final answer we need to add up the integrals for each part of the piecewise function whilst following that extra special formula from before. You know, this one: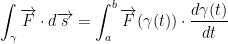 
Alright, let's do this!
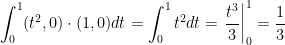
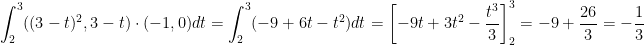
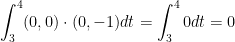
So then, our final answer is:
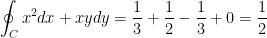
BUT WHAT ABOUT THE OTHER INTEGRAL!?
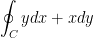
The professor says that, "we remart that the vector field F(x, y) = (y, x) is conservative, therefore since the unit square is simply connected, its integral over the perimeter (closed simple curve) is 0."
I don't 100% get this but, for the sake of time since it is now 7:13pm the day before the final, I'm gonna move on.
Question 12
Find
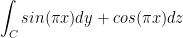
where C is the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1).
Very similar to the last question. The hardest part in my opinion is just figuring out how each point of the triangle connects.
As per the professor, we have:
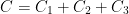
C1 is the line segment from (1, 0, 0) to (0, 1, 0).
C2 is the line segment from (0, 1, 0) to (0, 0, 1).
C3 is the line segment from (0, 0, 1) to (1, 0, 0).
The parameterizations of these segments, with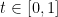 
, are:
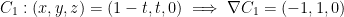
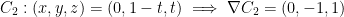
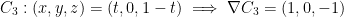
If you're having trouble figuring out how we managed to define each Ci function, look carefully are how we defined the line segments. Then think about what you'd need to change to go from one point in the line segment to the other. I hope that helps some...
Anyways, let's wrap this up!
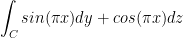
We just need to apply each line segment to the above equation and add up the results. To make things easier, let's run the numbers for each line segment one at a time.
Remember, this is pretty much just what we did back in the previous question with this formula:
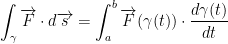
Alright, now let's apply that to each line segment!
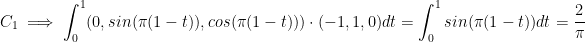
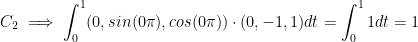
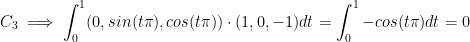
Now we have our final answer!
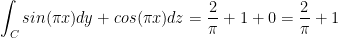
And that's it.
Question 13
Evaluate each of the following integrals:
1) 
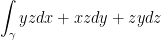where γ is the triangle with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1).
2) 
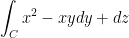where C is the parabola 
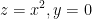from (-1, 0, 1) to (1, 0, 1)
For the sake of time, I'm skipping this question since it is very similar to the last two.
Question 14
Let P be the parallelogram bounded by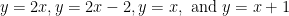 
. Evaluate:
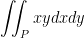
(Hint: Make a change of variables 
)
To start, it's hard to see how the parallelogram is bounded so I'm gonna rewrite it:
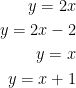
Next, let's make use of that hint the professor gave us. Let us have the following transformation:
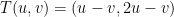
He notes that it is one-to-one and takes the rectangle P1 bounded by the following onto P:
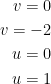
If you're wondering how we got those numbers, just plug in and solve based on y = 2x and the rest of those.
Next, we do a good ol' Jacobian like so:
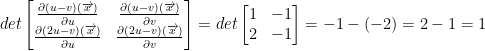
I'm not 100% sure why we do the Jacobian for this problem though... A quick search online says that the determinate of the Jacobian matrix,
"is used for when you want to integrate a function in a different basis, to make integration easier. For example, if you want to integrate across a circle, you would usually take the double integral in polar coordinates. Going to polar coordinates is a transformation, and thus has a Jacobian. When we integrate in polar coordinates, we stick an r unto the function we are integrating, this r is simply the Jacobian of the Cartesian -> polar transformation. This can be extended to any transformation however, if you want to compute the integral of a function in a different basis, you have to tack on the Jacobian of the transformation (as well as transform the integral) before you integrate." - Michael Kogan on Quora
Either way, we now have:
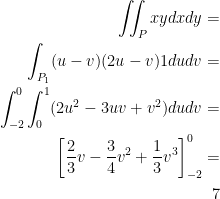
Question 15
Evaluate:
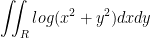
where R is the region in the first quadrant lying between the circles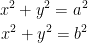 
with 0 < a < b.
It's really late. I'm stopping here for sleep. Good luck on the final everybody.
Question 16
Fuck
Question 17
Using again spherical coordinates in 
, calculate the volume of the sphere of radius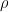 
, centered at (0, 0, 0).
The volume of the ball (i.e. of the sphere S2 in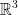 
) is given by the triple integral:
Here, we will use again spherical coordinates as follows:
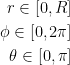
We then have:
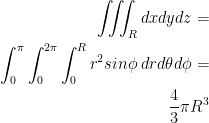
It might look intimidating but this integral actually isn't too bad to do by hand. I double checked it on my whiteboard and got the right answer.
