Question 1
For this first problem, I was a little perplexed by the solution our professor gave. He said to just use the dot product formula which is as follows:
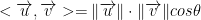
This of course confused the hell out of me. I wasn't quite sure how this formula was to be used to find the projection of vector v onto u. Luckily, in the Monday Meetings:3rd stream, he explains that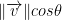 
gives us that projection of v onto u that we are looking for.
So then, we end up with this:
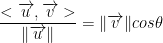= projection of v onto u
Now we can crunch the numbers like so:
Let v = (2, 1, -3) and u = (-1, 1, 1)
<u, v> = 2 * -1 + 1 * 1 + -3 * 1 = -4
The dot product is -4.
Now lets get the norm of u like so:
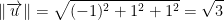
We then have the following answer for the projection of v onto u:
Going online, symbolab says that this is the scalar projection of our v onto u.
Question 2
This one is a little less obscure but still poorly written. To solve, we need to find the cross-product of vector -3i + 2j + k and vector k. Once we find that, it becomes quite obvious what λ needs to be for vector 2i + λj. At least, it will in a moment here. Observe:
Let v = (-3, 2, 1) and u = (0, 0, 1)
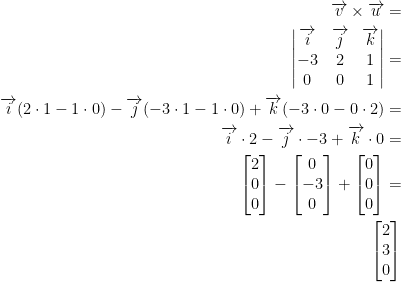
So then, we know that the vector (2, 3, 0) is orthogonal to vectors v and u. Looking at vector 2i + λj, we have (2, λ, 0). Simply replace λ with 2 and we now have a vector orthogonal to v and u! We did it yay!
Question 3
Finally! A question that's easy to understand just what the heck we gotta do!
We have the following:
Let v = i + j = (1, 1, 0), u = j + k = (0, 1, 1)
We need a unit vector that is orthogonal to these two vectors.
To begin, let us find a vector orthogonal to vectors v and u. To do this, we find the cross-product like so:
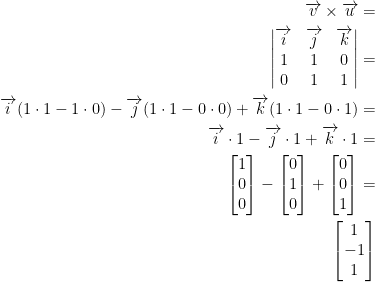
So then, our cross-product of v and u is the vector (1, -1, 1). In case this wasn't clear, the cross-product gives us a vector that is orthogonal to vectors v and u. However, we're not done yet! Now we need this as a unit vector which is a vector with a length of 1. Luckily, this is simple to compute! Just divide the result of our cross-product by it's length (or norm) like so:
And that's it! The answer is, as he put it in the solutions,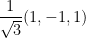 
. You could also distribute the fraction over the vector if you want. Either way works fine.
Question 4
This question gave me a bit of confusion. Mostly in figuring out the right way he wanted us to do this. Luckily, we got him to explain what he was looking for and it makes a lot more sense!
Firstly, check out this diagram:
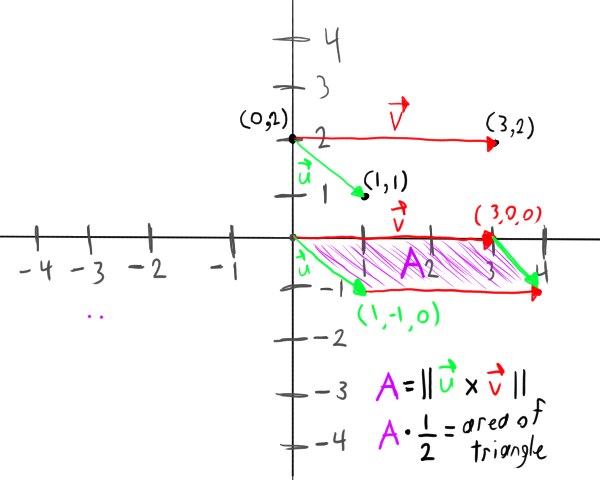
What we did here was take point (0, 2) as the origin. We then offset points (3, 2) and (1, 1) by point (0, 2).
Next, we need to find the area of the parallelogram formed by our newly created vectors u and v. To do this, we simply find the length (or norm) of the cross product between u and v. This gives us area A which is a parallelogram. But! We want the area of the triangle formed by these three points! Simply divide A by 2 and we have our answer.
Enough typing, let's crunch out these numbers like so:
Let u = (1, -1, 0) and v = (3, 0, 0). Notice that we add on a third dimension! This was intentional for we need a 3 dimensional vector to find the cross-product.
Let A be the area of the parallelogram form by u and v. We then have:
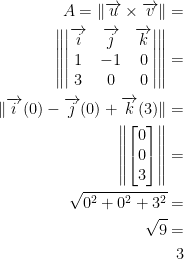
As such, the area of the parallelogram is 3. However! We need the area of the triangle! As such, simply divide A by 2.
The final answer is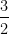 
which is precisely what the professor wrote on the solutions.
Question 5
This one threw me off slightly but it's quite simple. It does take a tiny bit of intuition to realize what's going on though!
First, let's observe what the question is asking us. It wants us to prove the following:
If you're anything like me, you immediately felt bad about yourself. At the same time, a part of you notices something. That something is the following:
Let v = (x, y). Then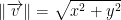 
.
Oh! We're just adding together the norm of three vectors! In that case, let us have the following:
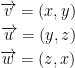
In that case, our right side of the equation is:
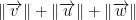
But what about our left side? I won't lie, this takes a little bit of intuition as well. What you'll realize is that we just add our three vectors and take the norm like so:
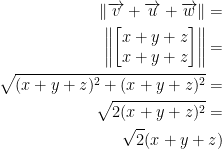
Now, this last part I don't fully get. He states that if we refer to the triangle inequality, we will see the following:
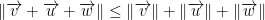
After looking online, I now know what the triangle inequality is. It is as follows:
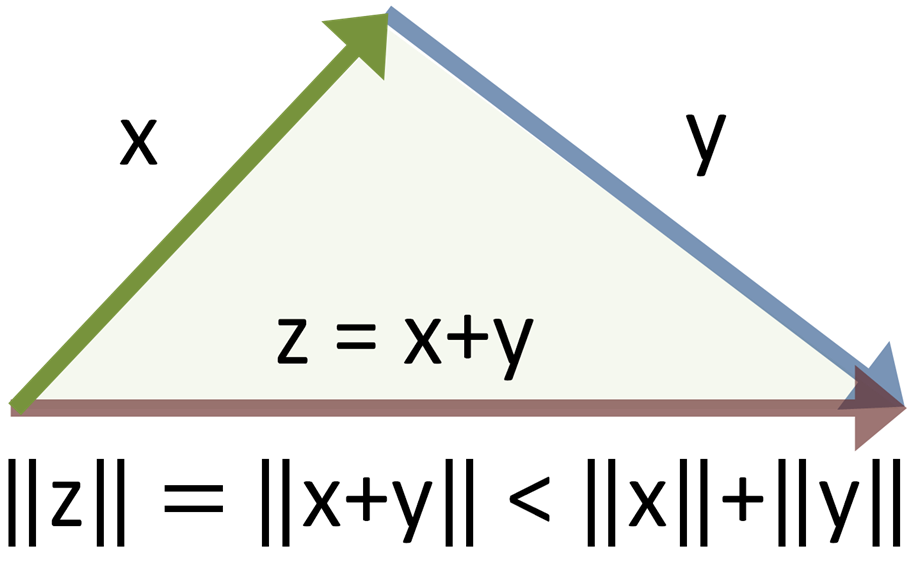
We of course expanded this to 3D space since we're working with the z componenet as well.
Question 6
Another question I wasn't so sure how to start.
So, we are asked to prove that two non-zero perpendicular vectors in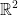 
must be linearly independent.
Firstly, vectors are linearly independent if the only way to achieve a 0 when adding them all together is to set their coefficients to 0.
Keeping this in mind, let us have vectors x and y that are two non-zero perpendicular vectors. Let us make the assumption that λx + μy = 0.
We then have the following:
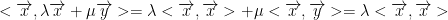
In case you're wondering why we removed μ<x, y>, the dot product of two perpendicular vectors is 0. In case you're further wondering why this is the case, observe the formula:
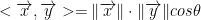
If two vectors are perpendicular, then θ is 90 degrees or π/2 radians. As such, cos θ gives us 0 whether we set θ to 90 degrees or π/2 radians.
Since x and y are perpendicular, we know that μ<x, y> = 0.
This of course leaves us with just λ <x, x>.
As such, for λ<x, x> to be zero λ must equal 0.
If you were to repeat everything we just did but with <y, λx + μy> you'll see that μ must also equal 0.
Therefore, λx + μy = 0 iff λ = μ = 0.
Since our coefficients must be 0, we can safely say that two non-zero perpendicular vectors in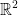 
must be linearly independent.
Question 7
We are asked to find all matrices in which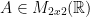 
such that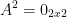 
To begin, let us have the following:
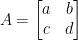
This also implies the following:
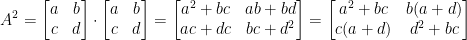
Now we need to know what values a, b, c, and d must take on to give us a 0 matrix. In order words:
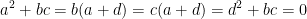
Right off the bat, we can see that if a + d = 0 then all that's left to worry about is that pesky bc.
We also know that det(AB) = det(A) * det(B). In this case, if the det(A) = 0 then det(A2) = det(A) * det(A) = 0 * 0 = 0.
As such, ad - bc = 0. We know this for if the determinate is 0 then we effectively have an area of 0 which is what the 0 matrix would have.
Question 8
This one isn't too bad despite the anxiety I am cursed with upon seeing it is a multipart question.
All we need to do is find what values t should equal to satisfy the following three subquestions. But first, let u = (1, t, 2) and v = (t, 4, 4)
a)
For what value must t be for the two vectors to be parallel?
My initial thought was perhaps we need the dot (inner) product. However, we should instead use the cross-product! If the cross-product between u and v is the 0 vector, then we know them to be parallel. Let us crunch some numbers then:
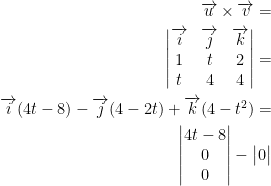
b)
Orthogonal?
c)
Make a 45 degree angle?
