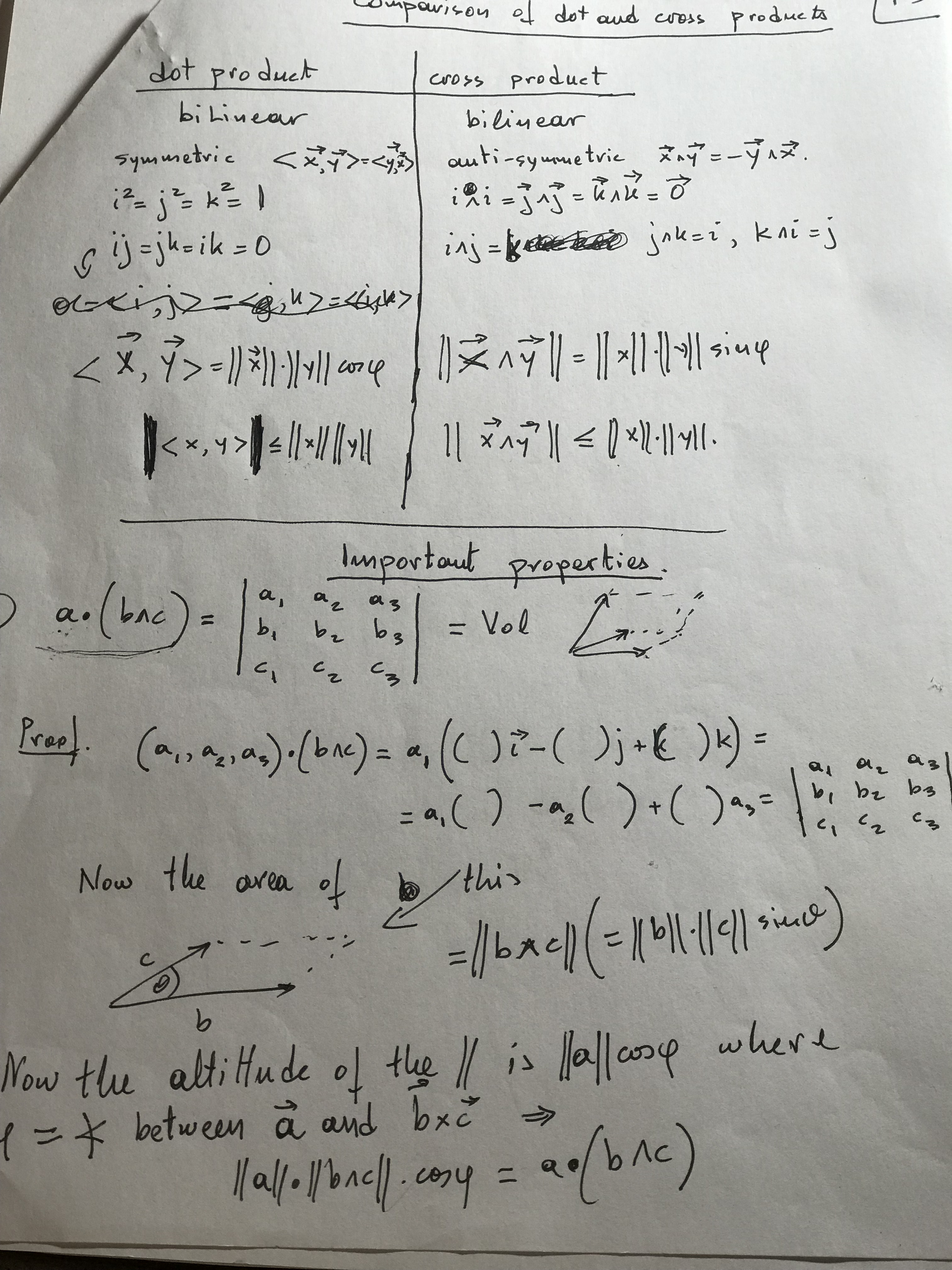3rd

Created Monday 15 June 2020

Quiz is on Wednesday at 10am under course documents. Send your answers as a PDF at his email.
He will accept exams up to 10:35am. So we have a 5 minute grace period.

ifarmakis@brooklyn.cuny.edu

Quiz will include the lines and planes stuff?

There are no curves.

Remember, final is 40% and each quiz is 30%.

Quizes are graded 100% maximum.

There will be 8-9 questions(?)

Hw Sol

HW2: #9

Someone asked about question 9 of HW 2.

I understand the idea. If the parallelogram from the determinant has an area of 0, then

He notes he meant to write -2 instead of just 2.

He drew the points and had (1, 5, 2) be the origin of the vectors.

for a he goes (-1 - 1, -3 - 5, 3 - 2) = (-2, -8, 1)
b = (-4, -6, 3)

HW2: #7

Just set the matrix to be:

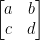
Simply multiply that by itself to get A².
Also, DETERMINATE! The determinate of A² must equal the deterinate of the zero matrix.
Remember, det(AB) = det(A) * det(B)
Since A² = 0
Then det(A²) = (det(A))² = det(0) = 0
So, det(A) = 0.

The determinate is how we got ad - bc.

HW2: #1

Let v = (2, 1, -3) and u = (-1, 1, 1)

He first finds the inner product of <u, v> = -2 + 1 - 3 = -4.

Then

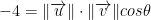
The projection of v onto u is literally just 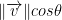. In a way, you can think of cos θ as rotating vector v to project onto vector u. With this, we solve:

HW2: #2

Just do this:

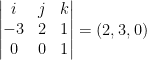
Remember, do the determinate stuff to solve this!

Now then, we need 2i + λ j to be parallel.
So then, 2i + λ j = (2, 3, 0)
As we can see, λ is 3.

HW2: #4

He says it's similar to exercise 9.

So, we have points (1, 1), (0, 2), and (3, 2).
So, take one of this points as our origin of sorts. Let's say we'll make it (3, 2).
Area of parallelogram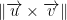

Let the vector from (3, 2) to (1, 1) be vector u. (-2, -1, 0)
And then vector v is from (3, 2) to (0, 2). (-3, 0, 0).
Then we just find the determinate and divide by 2. Remember, we end up with a parallelogram.

HW2: #5

He says there is no highschool algebra needed for this.
Notice how on the right side we have the formula for the length of each vector. On the left, we have the length of each of those three vectors from the right added together.
Putting this all together, we see that it is equal! I'll put more information on this in Homework:Homework 2.

Additional Notes

He tells us a few extra things he wants us to know.
dot product is symmetric.
cross product is anti-symmetric.
In dot product, i² = j² = k²= 1

It's a little hard to read the paper he showed us. He said he'll put it online later today for us to download.

For the Quiz

He says to really know the theory or else we'll have trouble. Don't forget about vector space, subspace, etc.

Professor Notes