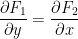Cheat Sheet

Created Wednesday 01 July 2020

Formulas are hard to remember so let's put them where we can find them at a moments notice.

Jacobian Matrix

It looks like this:

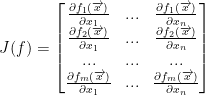
Gradient

Sorta like the Jacobian matrix but, instead, we have a single vector of partial derivatives. It looks like this:

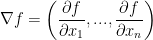
∇ is known as nabla. ∇f is looking for the gradient of f. The gradient is literally just that vector of partial derivatives. It's pretty much just the first row of the Jacobian matrix.

We can generalize the gradient like so:

Laplacian Operator

The Laplacian operator is just a triangle. The equation looks like this:

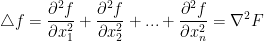
So, we take the second derivative of each input in regards to function f and add it all together. This is the equivalent of squaring the ∇f or the gradient of f.

In regards to Question 12 from Homework:Homework 4, a function is harmonic if it's laplacian is equal to 0.

Directional Derivative

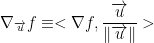
Where we find the inner (dot) product between the gradient of f and the normalized direction vector u.

To find the directional deriavtive for a certain point a, do this:

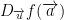
This just means we do this:

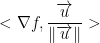
But we do:

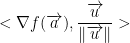
So, we pass a into our gradient of f and cross product that with our normalized direction vector.

To find the largest value of our directional derivative, do this:

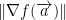
To find the direction that it occurs in, just divide the gradient by the largest directional derivative.
So something like:
This is the directional derivative:

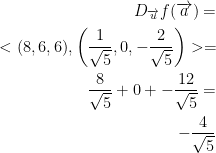
Largest value of the directional derivative

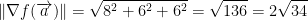
Direction that it occurs in:

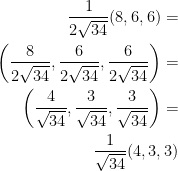
If this wasn't enough, homework 4 question 3 has a wonderful explanation!

Equation of a Plane

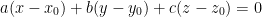
Where the coefficients (a, b, c) is a vector perpendicular to the tangent plane at x₀.

Normal Line

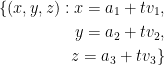
Critical Points

He says that we should know from calculus one that if a point is a maximum or a minimum then its derivative is 0!

As such, that's how we know if we have a critical point.

Hessian Matrix

This is useful in helping us determine whether or not our critical points are a local maximum, a local minimum, or a saddle point.

It looks like this:

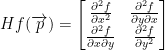
If we have the function 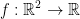we call the Hessian of f at the point p is the Hessian matrix (H stands for, "the Hessian" by the way):

If the function is differentiable, then the top-right and bottom-left elements of the Hessian matrix are equal.

We can find the determinate like so:

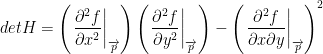
Furthermore, we can determine if a critical point is a local minimum or local maximum like so:

But what if the det H is less than 0? Then we have:

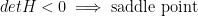
If the det H is equal to 0, then we have nothing to conclude!

Vector Space

• Additive Closure
• Scalar Closure
• Commutativity
• Additive Associativity
• Zero Vector
• Additive Inverses
• Scalar Multiplication Associativity
• Distributivity across Vector Addition
• Distributivity across Scalar Addition
• One

For details, see this webpage.

Dot (Inner) Product

Gives us a single scalar result. Good to note: Two vectors are orthogonal if their dot product is 0. Make sense because cos(π/2) = 0. That brings us to the actual formula:

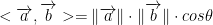
We can also multiply each corresponding component then add the result to get the dot product.

Projection

Continuing on the idea of a dot product, we can also find the projection of one vector onto another.

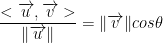gives us the projection of v onto u.
In particular, this is the scalar projection of v onto u. For the vector projection, we use a different formula.

Cross Product

The cross product gives us a vector that is orthogonal to two other vectors. Note, the cross product can only be done in 3D space.

The following is how you take the cross product for vectors v = (-3, 2, 1) and u = (0, 0, 1):

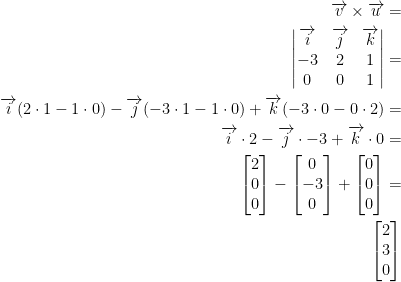
You are taking determinants. Also, don't forget that for j you subtract!

Determinants

A scalar value that we can compute from a square matrix. We denote it like so:
det(A)
where A is a matrix.
Geometrically, you can view it as the volume scaling factor of the linear transformation described by the matrix.

Normalize

When we want to normalize (turn into a unit vector) a vector, we write:

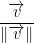
for some vector v.

Norm (Length of a vector)

Let v = (a, b, c)

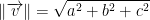
This works no matter the number of components of the vector v.

Triangle Inequality

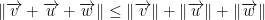
Linearly Independent

Vectors are linearly independent if the only way to achieve a 0 when adding them all together is to set their coefficients to 0.

Linear Map

A linear map (or linear function) must have the following property:

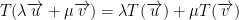
If it does not, then it is not a linear map!

Conservative

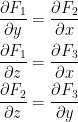
If these all hold, then the vector field F is conservative (for 3D space)

If working in 2D space, then just check if: