Homework 1

1) No. Real numbers are not a subset of rational numbers therefore 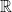cannot be a subspace of the set of rational numbers .
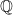Building on this, our professor's official solution is also no for 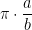is not rational.

2) No. Take the vector v = (x² + 3x + 1) and w = (-x² + 2x + 4).
v + w = (5x + 5). This result is not in the vector space of the set of all polynomials of degree >= 2. As such, we do not have a vector space.
In the professor's solution, they said that it is because 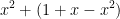is not in the vector space V. In case you didn't see it, expression simplifies to 1 + x which most certainly does not have a degree >= 2.

3) No. To be a vector space, a + (-a) = 0. However, the proposed nonstandard scalar multiplication would give us a + (-a) = a + a = 2a. As such, we do not have a vector space.
The professor also answered no. Let * be for the nonstandard scalar multiplication. In that case, (r + s) * a = r * a + s * a ⇔ a = a + a

4) No. Let a = (0, y, z). To be a vector space, a + (-a) = 0. However, we instead get the following:
a + (-a) = (0, y, z) + (0, 0 -z) = (0, y, 0) != 0
The professor also answered no. The reason is that there does not exist multiplicative identity for (0, y, z) if y is nonzero. As an example:

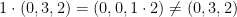
5) Both axioms for addition and scalar multiplication work here. If we have vectors v, w, and z each with a single element that is a rational number, then we have the following:
Addition:

Scalar Multiplication:

The professor states, "just check the properties." As such, I'm assuming my answer is correct.

6)

1. I got this one wrong. The real answer is no. This is because it is not closed under scalar multiplication. Say we have vector v = (x). Then 3 * v = (3x). However, if we take the derivative of this new vector then we have 3 which is NOT <= 1. As such, V is not a vector space.
2. I was also unsure of this one. In the case of scalar multiplication, if we multiply by 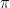then we would not have an integer!
3. I wrote no because v + (-v) != 0. However, the professor notes that V is indeed a vector space! He states, it is closed under both addition and scalar multiplication and check all other properties." Upon closer inspection, I believe he is wrong. My initial point still stands.
4. No. My answer is similar to the one above in which it can't be write due to how scalar multiplication is defined here. Let v = (x, y, z).
   1. 
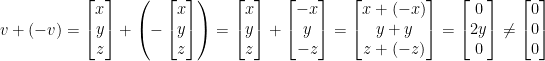
   2. He also states no because 2(x, 1, z) = (2x, 1, 2z) != (2x, 2, 2z)
5. I'm assuming yes. He also states yes. It loosely makes sense to me but I don't know enough about the properties of differential equations to confirm why. I need to research this more on my own.
6. I want to say no. He also says no but I'm not sure why. Once again, I need to research differential equations.
7. Yes.

7) I wasn't sure how to show this but the homework solution pdf does a great job. Essentially, you can first prove that V is closed under addition and scalar multiplication. Once you do that, the rest pretty much writes itself. I recommend writing this all out by hand to get a feel.

8) As with #7, we can show that the intersection of U₁ and U₂ is closed under both addition and scalar multiplication. In the words of the professor:
If 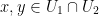then 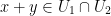. Also, 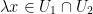for all .

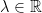9) One must be a subspace of the other due to the neutral element 0. They both must contain this therefore one subspace must be a subspace of another.
As for the professor's answer, it's a tad bit complex. Really think about this one!

10) I wasn't sure about this one but it's more obvious now. Let U = 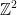. Then U is not closed under scalar multiplication. Why? Let v be some vector of U. Then 1/2 * v would give us a rational number that in not in the proposed subspace U.

11) This one also makes a little more sense after digesting it. Still a little weird so study it some more!