Created Thursday 11 June 2020
Foreword
He says that we don't have to wait until Monday to ask questions. He needs us to be specific though. Merely writing, "I'm having problem with the homework" isn't enough. He needs to know just what the issue is.
Any day of the week you can message him!
Determinants
Firstly, a unit vector is a vector v in which the length is 1. Or more mathematically:
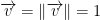
Suppose v is any vector != the 0 vector. Then the following gives us a unit vector:
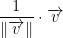
Then we also get the following:
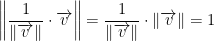
Now, on to determinants!
A determinant exists only for nxn matrices. In other words, a square matrix! Otherwise, there is no determinant.
Definition:
det() is determinant by the way
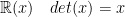
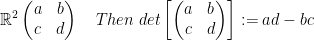
:= means by definition.
So then, we have this:
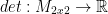
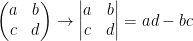
Notice we replace () with ||. This means we are looking for the determinant.
So then, what exactly does the determinant represent (geometrically at least)?
Let us have the following:
He goes through a very interesting proof to show how this is done. I'm not gonna write it all out right now but it all simplifies to show that we get ad - bc.
So then, the determinant of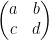 
is the area of the parallelogram spanned by the 2 vectors (a, b) and (c, d). This is what he drew out but I won't be doing that myself (due to laziness).
He then states that a determinant represents a volume! You can consider the area as the volume of a flat body.
3D Determinant.
We just found the determinant for a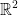 
but what about for the third dimension?
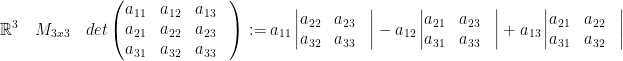
So, we have the first row act as coefficients and multiply by determinants on the two rows below.
You might be wondering if there is a pattern to when we should add or subtract. For each coefficient of the determinants, add the i and j values. If even, then add. If odd, then subtract. So, a11 is 1+1=2 which is even. Likewise, a12 is 1+2=3 which is odd. Therefore, we add the a11 and subtract the a12.
What if we have an even bigger matrix? We do the same thing! We just keep breaking it down to that 2x2.
Also, we don't have to take the first row. We could take the second or third but don't bother. Might as well just do the first one.
Also, he won't be proving this. It will be much too complicated right now.
In addition, he mentions it will take pages upon pages of work to find the determinant of matrices that are even bigger than this! For that reason, if we need to work with a determinant he'll just tell us what it is to save time. Or it'll be very easy to calculate.
Properties of the Determinant
First
For the first property, if we have two square matrices A and B...
det(AB) = det(A) * det(B)
Once again, the determinate of AB is just the determinate of A times the determinate of B.
Second
det(A) = det(AT)
What this says is that the determinate of the matrix A is equal to the determinate of its transpose.
This makes sense to me since if the determinate of just area and we're just flipping the matrix around when we transpose it, then the area should stay the same. We merely repositioned things but we didn't affect the scaling.
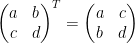
Third
det(Inxn) = 1
Why? Look at this:
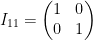
Remember, only that diagonal will have 1s. No matter the dimensions, the determinate of Inxn is always 1.
Fourth
If one row or column is a multiple of another row or column, then the determinate of A is 0.
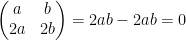
Fifth
He notes that this one is very important and we will be using it a lot!
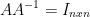
This reads that matrix A times the inverse of matrix A gives us the identity of dimension n by n.
He says cannot give us proof for this definition for when this inverse exists.
The matrix A has an inverse matrix A-1 if and only if 
So then...
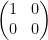does not have an inverse matrix because its determinate is 0.
However, 
does have an inverse materix because it's determinate is not equal to 0.
Cross-Product
The next and final big operation we can do with vectors!
The cross-product is exclusively for vectors in 3 dimensions!
We consider the vector space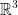 
(and no other vector space of some other dimension. do not forget this).
So then, how do we find this cross-product? Take the following:
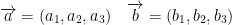
Remember, we have the basis vectors 
Definition: We define the cross-product 
as the vector...
By the way, I typed × but he couldn't do this on paper so he used a ^ sort of symbol to denote cross-product.
Now we have this:
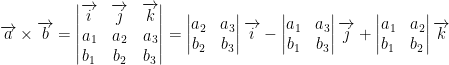
Remember, the determinates become a single scalar value. So we just take that scalar and multiply it by the vector. And then we just do simple vector addition!
Also, he wrote the cross-product as he did above to make it easier for us to remember how to do it.
Properties of Cross-Product
First
If you cross-multiply two vectors you get the following:
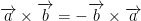
Why is this? Well, we merely flip the rows in the determinate from before like so:
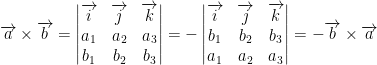
I believe I write that correctly. Might have to check the sign.
Either way, the cross-product is anti-commutative. In other words, a × b ≠ b × a
Continuing on, we also have the following for two equal vectors:
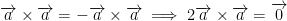
This also means that...
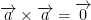
So then, anytime we cross-multiply a vector by itself we get a 0 vector.
Second
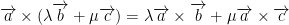
In other words, the distributive property holds here.
He also recommends we give this a try and check it. You learn by doing!
Third
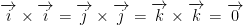
We also have this little interesting thing as well:
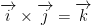
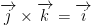
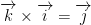
Notice how this is rather circular! Draw this as a circle with i on the right, j on the bottom, and k on the left. Then rotate clockwise. That's a good way to remember this.
Also, give this a go! You can check and see if it works.
Geometric Interpretation of the Cross-Product
Let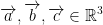 
Consider the following inner product:
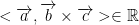
After some number crunching, we get this:
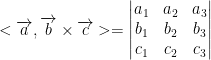
So the vector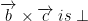 
to both 
and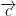 
. So it is perpendicular to the plane spanned by 
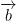and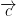 
.
Knowing what we know above, we also have this:
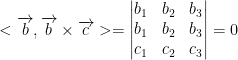
Notice how we have two rows that are equal! As we learned earlier, if this happens then the result is 0. Also, we know that if the dot product of two vectors are zero then we know that they are perpendicular!
Once again, the cross-product of two vectors gives us a vector that is perpendicular to the plane defined by two vectors!
Length of the Cross-Product
So, now that we've calculated the cross-product how do we get the length of it? We do the following:
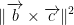
We read this as the square of the norm of the cross-product between vector b and c.
There's a bunch of math here and I couldn't quite see what he was writing. In any case, it all simplifies out like so:
The cross-product of two vectors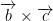 
is a vector in 
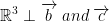and is of the length:
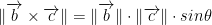
Remark
So if we were to draw out the vectors b and c, we can draw out a parallelogram in which:
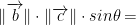the area of the parallelogram
θ is the angle between vectors b and c.
This boils down to a simple little theorem:
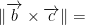area of the parallelogram which is spanned by b and c.
This Coming Monday
We will begin learning about the equations of the line and plane.
Quiz
Once again, the quiz is next Wednesday! At 10am on the dot. You will go onto blackboard to find our exam. Same place we find all of our lectures (course documents). You will have until 10:30 to answer the questions. We will then send it to an email address he will be giving us Monday.
HW
He posted homework. Go ahead and do that. This Saturday he will send us solution.