Created Wednesday 10 June 2020
Now we move on to the next topic of linear algebra: Matrices.
What is a Matrix?
We define a matrix 2x2 as an array of four numbers like so:
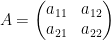
The previous is known as matrix A.
Each line we call them rows. Each column we just refer to as a column.
When defining the rows and columns of a matrix, we denote it like so: row x columns.
Each number in the matrix is known as an entry. For us, they will all be real numbers. No complex for us.
When we write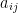 
the i indicates the row. While the j indicates the column.
So then, for the following matrix:
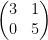
The entry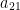 
is the entry 0. It is the second row and the first column.
This same principle applies to all matrices of any dimension.
Speaking of dimensions, a matrix has m rows and n columns. Or mxn.
So, a 3x1 matrix has 3 rows and 1 column.
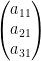
This of course gives us the form of a vector.
A 1x3 matrx on the other hand has 1 row and 3 columns.
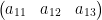
Any vector can be seen as a 3x1 or 1x3 matrix.
In general, we get this form:
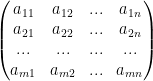
We can simplify this by writing:
Equality
Two matrices A and B are equal (written as A = B) if and only if they have the same dimensions and each corresponding entry must be equal.
So then, we have:
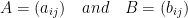
where i = 1 ... m and j = 1 ... n
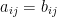
Operations between Matrices
Addition
First, we have addition with +.
Definition: If A and B are both mxn matrices (meaning they have the same dimension) only then can we add them.
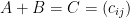
where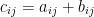 
The same applies to the additive inverse (aka subtraction).
Scalar Multiplication
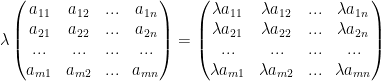
Just like in vector scalar multiplication!
Matrices as a Vector Space
Let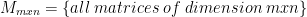 
then 
is a vector space.
Just like before with vectors, we have addition and scalar multiplication. We can also prove the other properties. As such, matrix M is a vector in the space of mxn dimensions.
Let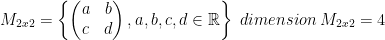 
The reason we have a dimension of 4 is because we have four basis matrices as we had with vectors. For example:
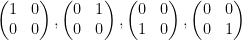
Each of the above are matrices of the vector space Mmxn.
We also have the following:
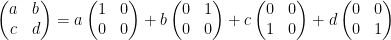
Next, to check if we have basis vectors (or I suppose matrices in this case) we must have linear independence.
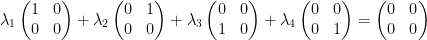
If the only way that we can get the zero matrix is if all of the lambdas are zero then we have linear independence.
This of course implies the following:
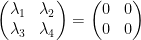
Types of Matrices
Square Matrix
The most interesting matrix is known as a square matrix. This is a matrix in which the number of rows = columns. Or m = x. Quite literally makes a square shape.
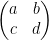is a square matrix.
In general, we have the following matrix:
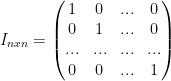
It's a little hard to type this out but imagine a nxn matrix that has a diagonal with all 1s.
This is known as a unit matrix.
Diagonal Matrix
As the name implies, a diagonal matrix is one in which only the diagonal has non-zero entries.
For example:
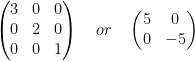
Zero Matrix
A zero matrix is one with all zeros denoted as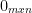 
Transpose of a mxn Matrix
Let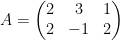 
The transpose of this matrix will go from mxn to nxm like so:
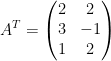
The T denotes that we have a transpose of a matrix.
Now then, if aij is in A, then aji in AT.
He says we won't be using the transpose of a matrix often but we still need to know it.
So then, rows becomes columns and columns become rows.
Multiplication of Matrices
We can multiply 2 matrices A and B only if the # of columns in A is equal to the # rows in B.
In other words, if the dimension of A = mxn and the dimension of B = nxp
So, we can multiply a mxn matrix by a nxp matrix if both of those n are equal. It doesn't matter what m and p are. Just those inner two n's matter.
So let's say we are multiplying a 3x2 matrix by a 2x5 matrix (notice that we have 2 and 2 which are equal). We do this:
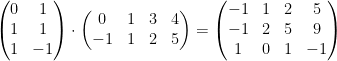
The way this multiplication works is that we take each row from the first matrix and find of dot product of it with each corresponding column in the second matrix. Remember, for a dot product (or inner product as per our professor) we multiply each corresponding element of two vectors and add the result together.
In general, we get this:
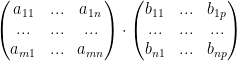
Then any entry in the resulting vector is represented like so:
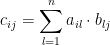
The variable l (lowercase L) is just all the entries in that row of the first matrix and the column of the second matrix.
Remarks on Multiplication
Firstly, matrix multiplication of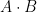 
is not commutative!
So then,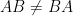 
Not only may they not be equal but it may be impossible to multiply them!
Let A be a 3x2 matrix and B is a 2x3 matrix.
AB works because A has 2 columns and B has 2 rows.
BA also works because it has B has 3 columns and A has 3 rows.
However, the resulting matrix may be different for AB than it is for BA.
On the other hand, let A be a 3x2 matrix and B is 2x1 matrix.
This works perfectly fine if we go AB! But what if we mix things around...
BA doesn't work because B has 1 columns and A has 3 rows. 1 != 3 so we can't multiply them!
On that note, we can always multiply 2 square matrices of nxn if they're the same size!
Another Remark
If A is a nxn matrix then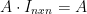 
Remember, is known as the unit matrix.
A Third Remark
For the 0 matrix...
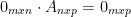
And a fourth remark!
Given a nxn (in other words, a square matrix) matrix A we call the inverse of A, the nxn matrix denoted by A-1 such that A * A-1 = Inxn
Not all square matrices have an inverse!
Now for an example.
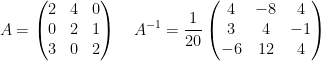
Check it! He requests that we do this to check out ability.
Multiply the two matrices and then do the scalar multiplication.
In this class, we won't have to worry about finding the inverse of matrices. This is more of a linear algebra course kinda thing. However, we will need to know if an inverse exists.
Important Announcement
Next Wednesday will be our first quiz! It will be at 10am in blackboard. It will not be on Monday like we had originally planned. He says to send him out answers as a pdf file in an email. The quiz will be half an hour long. If we can't do as a PDF, send to him as a picture. He won't grade if we're late.
He says there will be enough exercises to keep up occupied for 25 minutes.
Homework
For tomorrows HW, he will give us the answers Saturday so that we can have extra time to go over them.