Vectors Pt. 2

Created Wednesday 03 June 2020

This is a continuation of yesterday's lecture on vectors. These notes focus on the second vector video our professor has uploaded.

Video Notes

Fairly basic about 10 minutes in.
Basic vector addition: (3, 5) + (-1, 0) = (2, 5).

Real numbers we shall refer to as scalars (this comes from physics).
Definition: Let 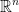= {(x₁, ..., x_n) 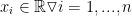} // not quite sure if I wrote this down correctly. The video is like a 144p YouTube vid back in 2006.
We define a scalar multiplication as:
=
(s, (x₁, ..., x_n)) = (sx₁, ..., sx_n)

What he means by the above is that we take a scalar number (let that be s) and multiply it by a vector of some size n. Each component of the vector gets multiplied by the scalar.

Properties of Scalar Multiplication

1. 1 * (x₁, ..., x_n) = (x₁, ..., x_n)
2. (a * b)(x₁, ..., x_n) = (abx₁, ..., abx_n) = (a*(bx₁₎, ..., a*(bx_n)) = a*(bx₁, ..., bx_n) = a*(b*(x₁, ..., x_n)). You can tack on anything you can think of really.
3. (a + b)(x₁, ..., x_n) = a*(x₁, ..., x_n) + b*(x₁, ..., x_n) = ((a+b)*x₁, ..., (a+b)*x_n) = (ax₁ + bx₁, ..., ax_n + bx_n)
4. (-1)*(x₁, ..., x_n) = (-x₁, ..., -x_n) = -(x₁, ..., x_n)

Definition: 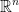equipped with the addition and the scalar multiplication is called a vector space. Or more accurately, a euclidian vector space.

When you see the plane 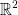, you can add and scalar multiply the points on this coordinate system. This is all a part of the vector space.

What is a Vector in Physics?

Definition: a vector is a quantity having both direction and magnitude (length).

The image vector is an arrow. Quite literally just an arrow as you would draw on a piece of paper.
Vectors are used to represent forces in physics for example. Magnetic field is a vector. Velocity is a vector due to it having both speed and also a direction that we are moving in.

Law of Parallelogram

When adding two vectors (such as vectors representing velocity) we put them together in a way that represents a parallelogram.

Vector Equality

Two vectors are equal if and only if they have the same length and the same direction.

More Vector Stuff

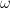= slope of 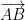is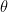
The w looking letter is called omega.

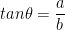
A vector in physics corresponds to a vector starting at 0 and ending at the point (a, b).
All vectors will have a common origin. In a 2D plane, that would be (0, 0). Any free vector will be one that starts at the origin and goes to a point.

The mathematical vector corresponds to a given point (a, b).

All free vectors of corresponds to points .
From now on, we will examine the space 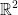.