Created Monday 08 June 2020
This is the fourth video our professor has uploaded.
We start the video by continuing our discussion of linearly independent vectors.
As a recap, we have two linearly independant vectors if the only way to add them to get a 0 vector is when their scalar coefficient are 0 as follows:
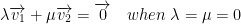
Definition: Let v1, v2, ..., vk be vectors in V. We call the linear span of these vectors:
lin. span. {v1, ..., vk} = 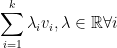
Then the linear span {v1, v2, ..., vk} is a vector space.
Let 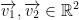 ,
, 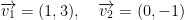
linear span of { } =
} =
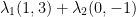 } =
} = {
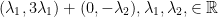 } =
} ={
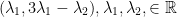 } =
} = 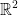
How about an example that is not 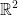 ? Observe:
? Observe:
Let v1 = (1, 3) and v2 = (-1/3, -1)
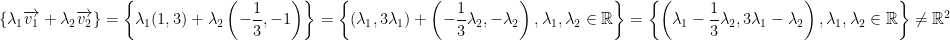
Notice how v1 and v2 are multiples of eachother!
Definition: If 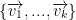 are vectors of space V such that:
are vectors of space V such that:
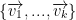 are linearly independent
are linearly independent- linear span
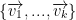 = V
= V
=> we call 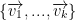 a basis of V and we call the number k the dimension of V and we write dimension of V = k. In otherwords, the number of vectors we have in our linear span is the number of dimensions we have for our basis.
a basis of V and we call the number k the dimension of V and we write dimension of V = k. In otherwords, the number of vectors we have in our linear span is the number of dimensions we have for our basis.
dim V = k
We know that the vectors (1, 3) and (0, 1) are linearly independent. But how do we check this?
Let 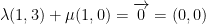
We need to prove that both lambda and mu are 0.
So, we have this:

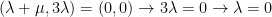
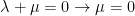
We such, we proved that these two vectors are linearly independent.
Remember, whenever we want to prove something we go immediately to the definition. Then we see if it applies to the problem we're working on. You will need to know your theory very well to make it through exercises.
Now then, why can any  be written as a linear combination of (1, 3), (0, 1)?
be written as a linear combination of (1, 3), (0, 1)?
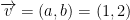
Find 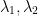
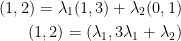
Now we can solve for the lambdas!
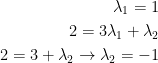
With this, we can write (1, 2) as a linear combination of the vectors: 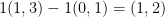
Considering this, we have the following:
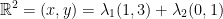
Since we can write any other vector from this two vectors, we have a basis.
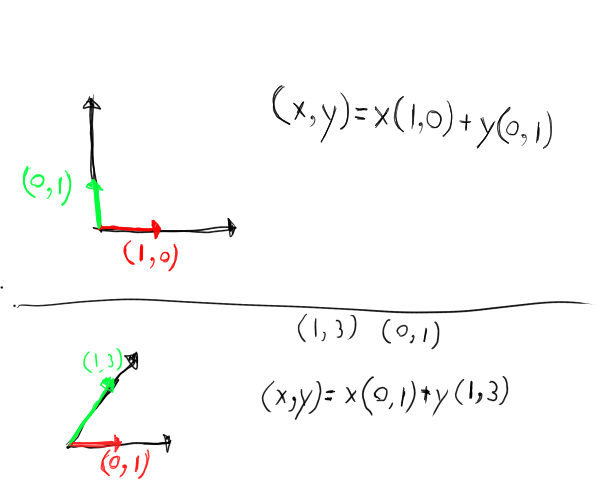
The diagram above shows basis vectors in action.
This applies to any dimension! 1D, 2D, 3D, 4D, 5D, ..., nD.
Linearly independent vectors are basis vectors.
More on Basis Vectors
For 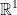 , (1) is a basis vector and so is (-10) for any other vector can be written as a multiple of it. For example,
, (1) is a basis vector and so is (-10) for any other vector can be written as a multiple of it. For example, 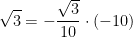
However, (1) is known as the natural basis.
For 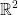 , we use two vectors:
, we use two vectors: 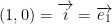 and
and 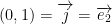
Likewise, we also have basis vectors for 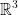 like so:
like so:
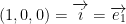
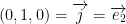
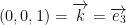
Finally, we have 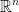
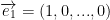
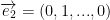
...
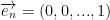
This all make up the natural basis in 
And Even More on Basis Vectors...
The following is a linear combination of the basis vectors:
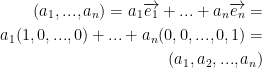
If 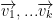 is a basis for V then any vector
is a basis for V then any vector 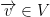 is written as a linear combination (sum):
is written as a linear combination (sum): 
I couldn't quite tell if I got that formula written correctly. The camera is very blurry.
Example of Vector Space Where It Cannot be Written Using Coordinates
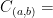 {all continuous functions
{all continuous functions 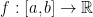 }
}
This reads that we have a set C and continuous function f from a to b that maps onto R.
We want to prove that C is a vector space. How do we do this?
For addition +, we have functions f and g. 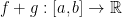 such that
such that 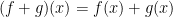
For example:
We have the 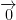 function.
function. 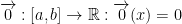
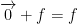 which read the 0 vector plus any function f is equal to f.
which read the 0 vector plus any function f is equal to f.
What about the additive inverse?
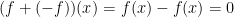
We also know it is commutative and associative in regards to addition
What about scalar multiplication?
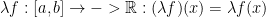
So, that works just fine as well!
So, we have a vector space. But! And then he says we can't have a set of something. I couldn't make out what he was referring to.
He goes on to say that we have an inifinite number of basis.
Inner Product or Dot Product
Yay my favorite!
Definition: The inner product is denoted by < , > : V * V 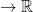
This reads "< , > is a function that..."
Also, 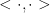 is the inner product! The dots are placeholders for numbers we input.
is the inner product! The dots are placeholders for numbers we input.
< , > is not an operation though.
So, we have the following:
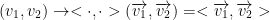
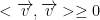 it is = 0 only if
it is = 0 only if 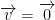
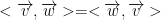 which means it's symmetric.
which means it's symmetric.- Most importantly, the inner product is bilinear.
What do we mean by bilinear? Observe:
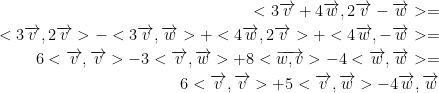
By the way, due to symmetry we can combine <v, w> and <w, v> as seen in the equation above.
If you have 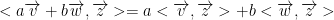
The av + bw is linear and so is the z. Since both are linear, we having something that is bilinear.
Continuing on...
In 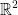 the inner product:
the inner product:
Suppose 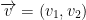 and
and 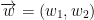
For the following, we take the product of the corresponding coordinates.
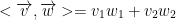
Here is an example of what we just did but with actual numbers:
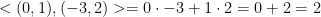
Furthermore:
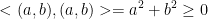
The inner product is 0 only if a and b are both equal to 0.
Likewise,
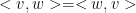
We can make this more general as well. For example:
For 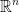 let
let 
When finding the inner product, we get the following:

Norm
Next, what is a Norm in a vector space?
Let Y be a vector space.
The norm is 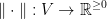 such that:
such that:
- The norm of any vector v is positive. Also can be written as:
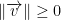 .
.
- It is only equal 0 if
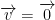
- It is only equal 0 if
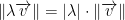
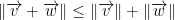 this is known as the triangle inequality.
this is known as the triangle inequality.
In 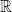 , the absolute value || satisfies all 3 of the above so in the vector space
, the absolute value || satisfies all 3 of the above so in the vector space  the absolute value |*| measures length or distance between points! (The * is just a standin for some value).
the absolute value |*| measures length or distance between points! (The * is just a standin for some value).
We can check that in 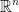
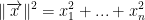
Knowing this, we get something similar to that of the Pythagorean Theorem:
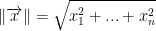
So then, let's say we want the length of (a, b). Then we do this:
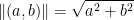
Let the following be a vector space: 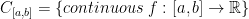
Prove that 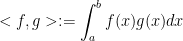
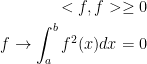
 has also a norm
has also a norm
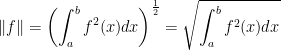
We have to check if this is a norm in  .
.
As we can see, the norm and inner product can be applied to any vector space!
The video ends here.