Inner Prod Norm Pt. 2

Created Tuesday 09 June 2020

An inner product is a function such that we can take any two vectors and get a real number.
The norm is also a function that gives us a non-negative real number.

So then, let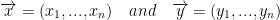

Concerning the norm, we have:

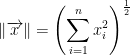
Properties of Inner Product (Dot Product)

Let V be a vector space and we have an inner product denoted as such: < , >.
Then we have the following theorem:
For any pair of vectors, x and y in V:

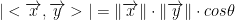
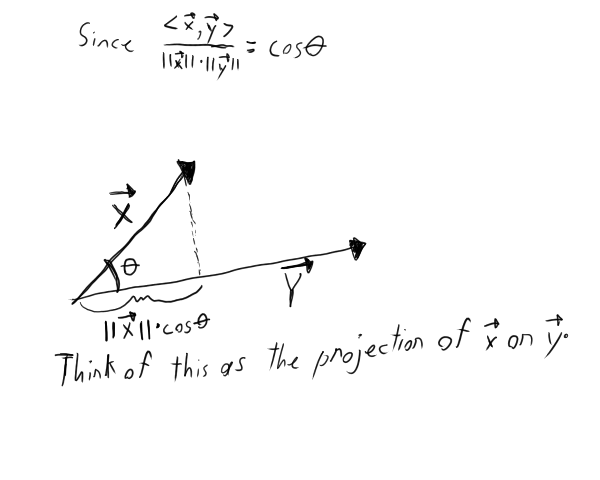
where theta is the angle between the two vectors x and y.

Proof #1

In the case of refer to the following image:

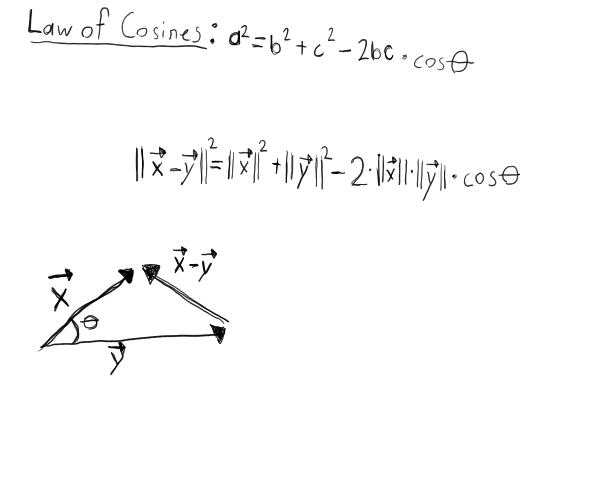
Continuing on from this...

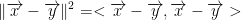
We can then multiply this out using bilinearity!

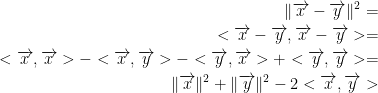
With this, we can do the following:

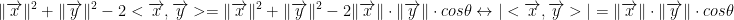
Notice we took the absolute value of |<x, y>|. He gave a reason for this but I didn't 100% understand why.

Example

Find the angle between the two vectors i + j + k and i + j - k.

Remember, i, j, and k are basis vectors.

i + j + k = (1, 1, 1)
i + j - k = (1, 1, -1)

Now let's find their inner product.

Now let's find the norm of each vector:

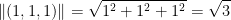
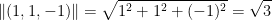
Knowing the following: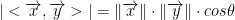
The above is a very important theorem by the way! Remember it!
We get this:

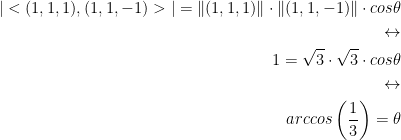
Remark 1

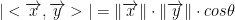
If 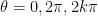then the vectors are parallel! So we don't get any angle between them.
So then, if we have parallel vectors then we have the following:

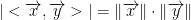
because cos(0) = 1.

If there is no angle between two vectors then they are parallel!

Remark 2 (More important he states)

Let 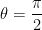or any multiple of pi/2. In this case, 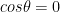. Then our formula becomes:

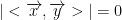
Definition

If 2 vectors of vector space V satisfies:

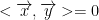
then we say that the two vectors are orthogonal meaning they are at right angles of each other.

Remark 3

Since the inner product in the following form:

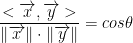
Another Definition

Suppose that vectors 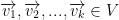where V is a vector space.
We say that the vectors above are orthonormal if and only if they satisfy the following two conditions:

1. The length of each vector
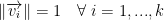
   1. This should be read as, "for any i from 1 up to k"
2. For any two vectors 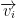and 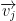they are mutually orthogonal for any i != j

As an example, the base vectors (1, 0) and (0, 1) are orthonormal.
In three dimensions, we have (1, 0, 0), (0, 1, 0), and (0, 0, 1) are all orthonormal.

Proof for Any Vector Space

1. For any two vectors 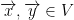where V is a vector space, we get:
   1. 
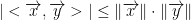
   2. This is known as the Cauchy-Schwarz Inequality

More Proof:
Let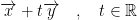
and set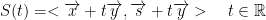

First make the observation that S(t) >= 0. It cannot be negative.

Then we can multiply using bilinearity:

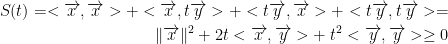
So then, S(t) is given by a quadratic polynomial.
Now then, for this to be true the quadratic equation S(t) = 0 must have at most 1 root solution.

Quick review: The discriminant helps us to determine how many solutions there are to a quadratic equation. It is that part under the sqrt. A positive discriminant indicates that we have two distinct real number solutions. A discriminant of 0 denotes a repeated real number solution. And a negative discriminant indicates that neither of the solutions are real numbers.

Also remember, a quadratic takes the form: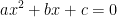

The discriminant 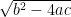must be 0 or negative.

Based on our formula above, we have:

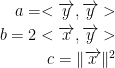
Based on this, we have the following discriminant:

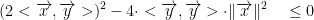
By this reasoning we have:

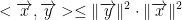
Now We Get The Following:

Since 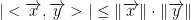and they are both bigger than 0 by the way!
The is a reason that

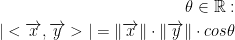
Proof:

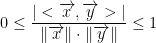
Moving forward... Let us say we have this set:

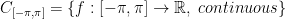
C is a vector space.
Also:

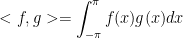
and the norm:

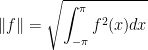
Find in vector space V two or more orthogonal vectors.
The professor says, "I claim that..." and then writes this:

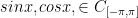
He will prove that sinx is orthogonal to cosx. This can also be written as:

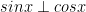
The upside-down T looking symbol is the perpendicular symbol. If two vectors are perpendicular then they are orthogonal.

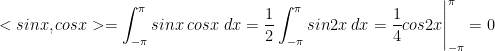
As such, sinx and cosx are orthogonal!