Created Monday 22 June 2020
We shall finish with limits and learn what the continuity of the vector function is.
In a vector space, we only have vector addition and scalar multiplication. We can't divide two vectors as well as you may have inferred.
Theorems or Properties of Limits
Assume we have a space of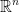 
a function f that takes us from that 
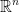space to a 
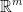space.
In other words: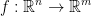 
Next, let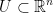 
be an open set and let 
. Vector a in this case is either in U or on the edge/border of it.
Now for limits.
Let us have the following open interval:
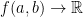
And yes, I do mean interval and not a vector as we've been used to.
Now then, we also have this:
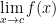
Our professor then states that we must check the following properties:
1) (x and a are in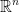 
by the way!)
If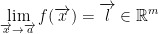 
and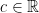 
we get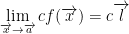 
2) If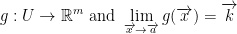 
Then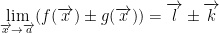 
3) Since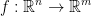 
is a vector function, we can think of it as: 
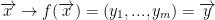. Remember, y is the image of vector x under the function f.
It's also good to note that each yi is an algebraic expression of the vector x. In fact, it is good to note this because we can take (y1, ..., ym) and write it as this:
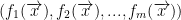with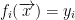 
Example
So, let's say we have the following: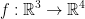 
Now then, say we have this: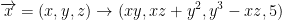 
As per property from above, we get this:
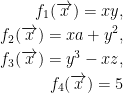
Further Definition
So then, we have the following:
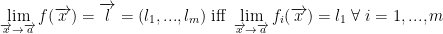
Proof of 2
I believe he's referring to the second property from before.
Anyways, let's begin!
Let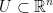 
and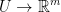 
where under the right arrow we have 'f, g'
We also have this:
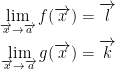
Okay now for something rather lengthy:
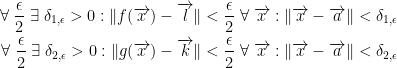
Now then, we want to prove that the limit of the sums is the sum of the limits. How do we do this? Like so:
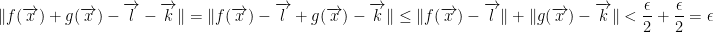
If you were wondering why we had ε/2 earlier, the above equation is why. In case that's not obvious, it's so we can add ε/2 to just ε.
Now then, we wish to take the minimum of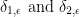 
.
So, we get this:
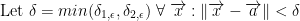
This is the proof he says.
Note on HW
He says that this upcoming Thursday (06/25/2020) he will post the answers to homework 3. Also, the next homework will be uploaded as well.
Sample Exercises
Example 1
Prove the following:
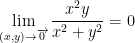
This is rather easy back in single variable calculus but now we must take into consideration two variables! Hence the multi in multivariable calculus.
Anyways, what the previous limit gives us is a function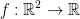 
Solution
First off, we know that x2 is always positive or 0. In other words:
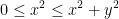
Notice that we also tacked on the y2 there.
Also,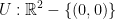 
. (0, 0) is the origin.
Knowing what we know now, we can infer the following:
Multiplying everything by y, we have:
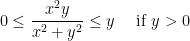
Likewise, if y is negative then we have:
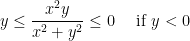
You may have noticed something interesting here. So, if x and y are both approaching 0 then we are bounded by those equations we just wrote. You might remember a little term known as the squeeze theorem.
So then, by the squeeze theorem we can see that the limit is 0!
Replace the y's with 0 in the previous two equations and you'll that it is indeed 0.
Example 2
Solve the following limit:
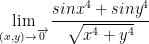
Quick aside:
Firstly, remember from Calculus 1 that:
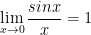
Thinking about this carefully, we see that:
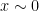
where the ∼ is a weaker = sign essentially. Moving on, we have:
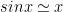
If not that, then:
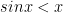
We can apply what we just discussed in the aside like so:
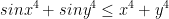
As such, our final answer is: 0. Yup. Just zero.
You might be wondering why 0? How did we glean that information? Well, if our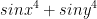 
is less than or equal to 
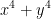then what happens when x and y approach 0? They become 0! That is my own interpretation at least. Here is what the professor wrote:
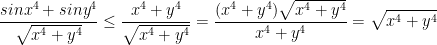
Then of course,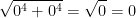 
Example 3
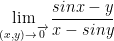
My first instinct was to split the fraction into 2 different ones with the numerator sinx and -y. However, the professor shows us the following:
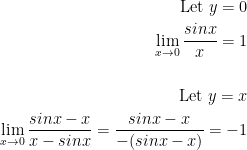
So, we have the limits 1 and -1. This isn't good! As such, THE LIMIT DOESN'T EXIST!
And that is our solution.
Example 4
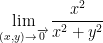
We shall do something similar to what we saw in example 3. Observe:
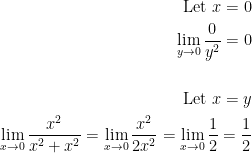
So then, we have the limits 0 and 1/2. Since they are different, the final solution is that THE LIMIT DOESN'T EXIST!
Continuity
Only 3 minutes of the lecture left. We shall end it with a quick definition of continuity.
Let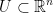 
Then: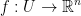 
f is continuous at a iff 
f is continuous iff 
Also, remember that the sum of two continuous functions is a continuous function. The same applies for the difference and also the multiples of continuous functions.
We can't multiply/divide unless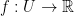 
. Notice, R is in 1 dimension.