Created Friday 03 July 2020
I accidentally watched the Path Integral-Green Theorem video first. Now I understand why things felt so complicated towards the end...
Anyways, let's integrate and stuff.
Double Integral
We have the function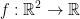 
.
When we write a double integral, we write:
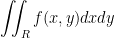
Where R is a domain in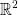 
.
So, when we write
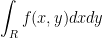
We mean the volume above R and under the graph of f.
In other words, we find the volume of the space above our domain R and under the surface defined by our function f.
I want to stretch once more that R is some region. It is our domain. We're gonna be using it alot so please remember what it is.
Example
If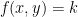 
.
So, it's a constant function.
Now then, we have the following diagram:
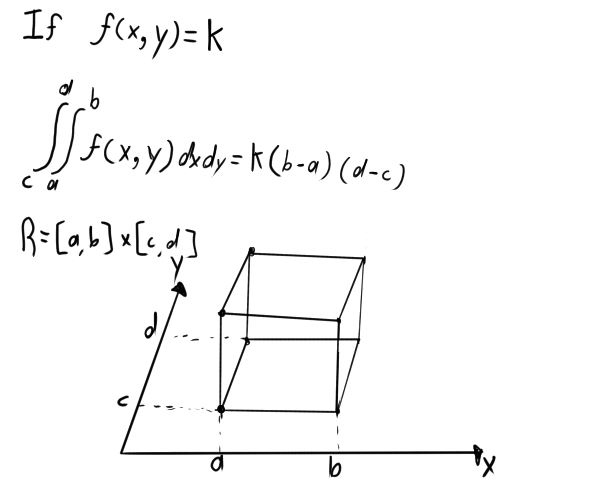
As you may be able to see, we end up getting the volume of a cube.
Moving forward, so we have the following:
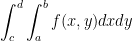
The order of the integrals shows the order of integration.
So, the above double integral actually implies the following:
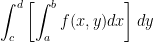
Putting this into practice, let's reuse the function we had for the cube. So, f(x, y) = k.
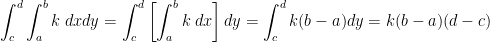
How does this get us volume?
Real quick, remember back in Calculus 2 how we used a bunch of rectangles to approximate the area under a curve? Well here, we just use a bunch of squares (at least, for dxdy).
We can refer to a specific square with i and j similar to how we refer to a specific element in a matrix.
That's just a quick and dirty explanation but it'll do. He also wrote a limit to show how this is calculated but I didn't copy it down.
Fubini's Theorem
If f is continuous over the domain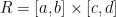 
then
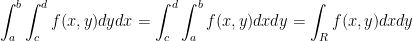
So then, if we swap around the integrals then nothing changes. So, we could integrate first for y and then x. It'll be the same if we integrate first for x and then y.
Example:
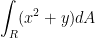
dA is the elementary area. So, it'll be dydx or whatever. Also, the above it a double integral despite there being only one integration sign.
Anyways, take the following: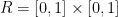 
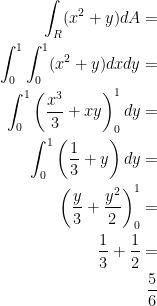
So, the answer is 5/6. We'd get the same thing if we decided to do dydx instead of dxdy.
In addition, if
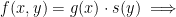
that by Fubini's Theorem
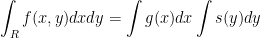
Our professor then draws the following regarding derivatives:
Theorem:
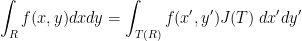
Remember, J is the Jacobian matrix. So, we take the Jacobian matrix of the transformation.
Example 1
Suppose we have the following:
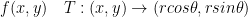
Of course, these are polar coordinates with the familiar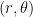 
.
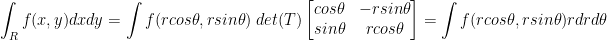
Also, if it wasn't obvious:
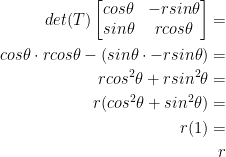
And Another One (Example)
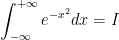
To solve this, we need to use double integrals. Let's observe how.
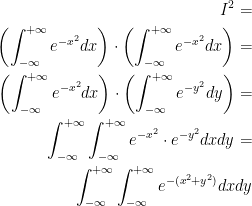
To solve this now, we use polar coordinates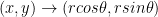 
This transformation, as we saw earlier, has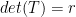 
.
Remember,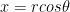 
and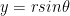 
.
Continuing from the big integral we were just doing, we have:
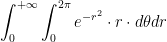
By Fabini's, we have:
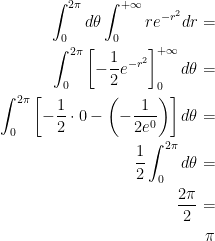
Bringing it all together, remember that we were calculating all of this from just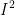 
. So, we have 
.
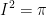As such,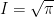 
.
Once more, we have:
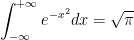
As our professor notes, we could not obtain this answer without the help of multivariable calculus!
Triple Integral
Similar to the double integral but now we have something like this:
So, our f function represents something in 3D space. Similar to how we added up squares to get the volume of the double integrals, we add up cubes to get the volume of something in a triple integral.
