Remember basic boolean logic. Y'know, AND, OR, and NOT. All of which can be described via a truth table.
The AND operator is also known as a Boolean Product.
The OR operator is also known as the Boolean Sum.
To denote a NOT, we use the prime mark. So, NOT X is denoted by X1 where 1 is prime (Note, we don't use 1 to represent prime. I wanted to use a backtick to represent prime but it was too small to see. From this point onward, assume super 1 is prime unless otherwise specified).
A boolean function has
- at least one boolean variable
- at least one boolean operator
- at least one input from the set {0, 1}
- produces an output that is also a member of the set {0, 1}
When figuring out the truth table for a Boolean function such as F(x, y, z) = xz1 + y, we can do so by constructing a truth table and sticking to rules of precedence that boolean operators have. NOT has the highest precedence, followed by AND, and then finally OR.
We can also simplify our boolean functions via the identity laws.



Also, don't forget about good ol' DeMorgans Law!
(xy)1 = x1 + y1
(x + y)1 = x1y1
Exercise 1
Construct truth tables.
Answers:
a) yz + z(xy)1
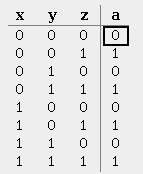
b) x(y1 + z) + xyz
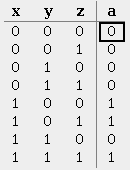
c) (x + y) * (x1 + y)
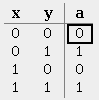
Exercise 22
From the given truth table, write a boolean expression in sum-of-products form.
There are two canonical forms for Boolean expressions: sum-of-products and product-of-sums.
For sum-of-products, ANDed variables are ORed together like this: xy + xz + yz
For product-of-sums, ORed variables are ANDed together like this: (x+y) * (x+z) * (y+z)
Getting the sum-of-products is easy! Just construct a truth table and then AND together variables where there is a 1 result. Sum all of those ANDs together to obtain the sum-of-products!
Answers:
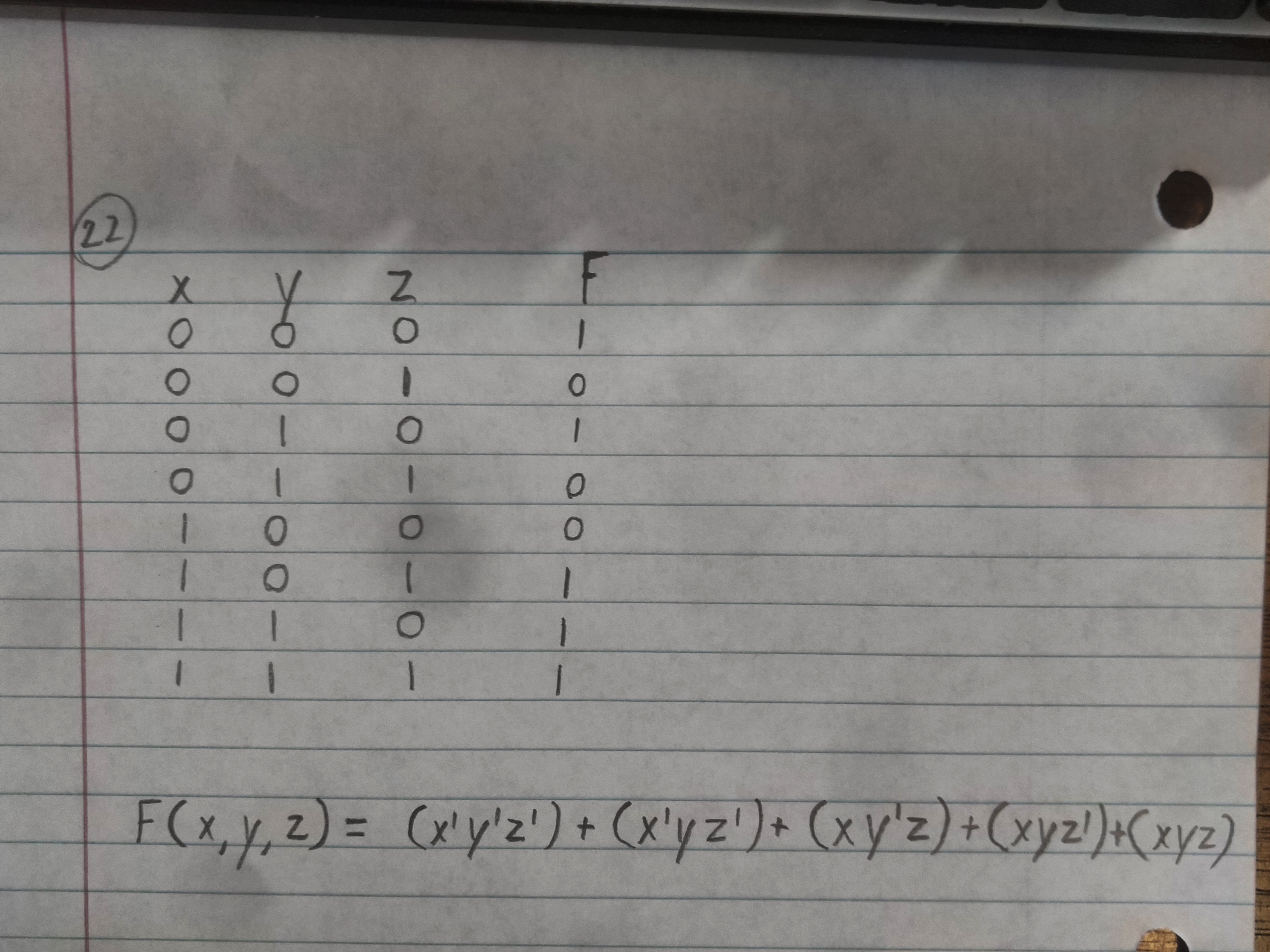
Question 6
The rest of the questions are not from the book but are straight from our professor.
Use logisim to show that the NAND gate implementation of the AND function is equivalent to the AND gate.
Remember, NAND gate is literally just a NOTted AND gate.
It's also important to note that any gate can be created via just NAND gates! This is great for NAND gates are cheaper to create.
To create an AND gate from NANDs, just use two NAND gates.
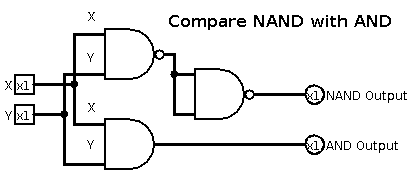
Question 7
Use logisim to show that the NAND gate implementation of the OR function is equivalent to the OR gate.
To create an OR gate from NANDs, just use three NAND gates.
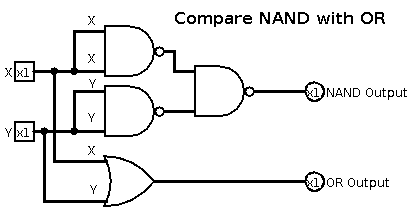
Question 8
Use logisim to show that NAND gate implementation of the NOT function is equivalent to the NOT gate.
Very simple. Just use a single NAND and plug the variable into it twice.
Question 9
Use logisim to show that the Associative Law holds.
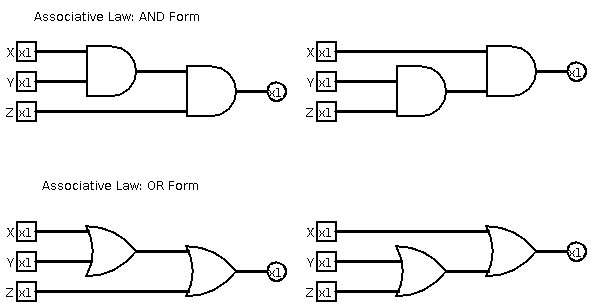
Question 10
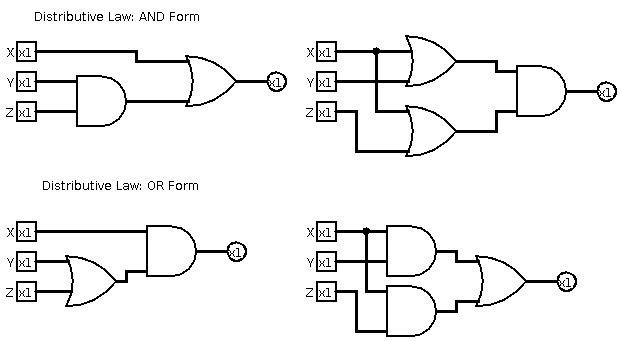
Use logisim to show that the Distributive Law holds.