Exercise 44
Use arithmetic shifting. This is very simple. Have you noticed how everything is done in powers of two for binary? Well, to double a value just shift all bits to the left. To divide, shift to the right.
Answers:
a) 000101012 = 2110
To double this, shift everything to the left.
001010102 = 4210
b) 011101112 = 11910
To quadruple this, shift to the left twice.
1110111002 = 47610
c) 110010102 = 20210
To divide in half, shift to the right once.
11001012 = 10110
Exercise 47
For this exercise, we need to make use of floating-point representation (using a 14-bit format, 5 bits for the exponent with a bias of 15, a normalized mantissa of 8-bits, and a single sign for the number).
Signed magnitude, one's complement, and two's complement deal with signed integer values only. Without modification, thees formats are not useful in scientific or business applications that deal with real number values. Floating-point representation solves this (Mostly. As an aside, floating-point numbers are an approximation and really wouldn't be good for dealing with business applications. You need actual decimal arithmetic to deal with this).
Floating-point numbers allow an arbitrary number of decimal places to the right of the decimal. They are often expressed in scientific notation:
0.125 = 1.25 * 10-1
5000000 = 5.0 * 106
Computers use a form of scientific notation for floating-point representation. Numbers written in scientific notation have three components:
sign Mantissa Exponent
+ 1.25 * 10-1
Computer representation fo a floating-point number consists of three fixed-size fields:
Sign | Exponent | Significand (some people say mantissa instead albeit they technically don't mean the same thing)
The one-bit sign field is the sign of the stored value.
The size of the exponent field determines the range of values that can be represented.
The size of the significand determines the precision of the representation.
In a simple 14-bit model, the exponent field is 5-bits, the significand is 8-bits, and the sign is 1-bit.
The significand is always preceded by an implied binary point. Thus, the significand always contains a fractional binary value.
The exponent indicates the power of 2 by which the significand is multiplied.
Simple example:
32 is 25. So, in binary scientific notation we have:
3210 = 1000002 = 1.02 * 25 = 0.12 * 26
With the above info, we know the exponent must be 6 in binary so 001102. Our significand is 10000000.
As such, we have this as our resulting 14-bit floating-point number:
Sign | exponent | significand
0 | 00110 | 10000000
We can represent 32 in a multitude of different ways but this causes confusion. As such, the first digit of the significand must be 1 with no ones to the left of the radix point as we see above. This process is known as normalization which results in a unique pattern for each floating-point number.
We also want to account for negative exponents. To do this, we shall use a biased exponent. Since we are using a 5-bit exponent, we shall use a bias of 15 or excess-15 representation.
In our model, exponent values less than 15 are negative, representating fractional numbers.
Let's look at our 32 example again.
3210 = 1.02 * 25 = 0.12 * 26
With excess 15 biased exponent, we add 15 to 6 thus giving us 2110 = 101012. So then, we get the following:
0 | 10101 | 10000000
Answers:
a)
100.010 = 11001002 = 0.11001002 * 27 = 0 | 10110 | 11001000
0.2510 = 0.012 = 0.12 * 2-1 = 0 | 01110| 10000000
b)
// notice, to match the exponents the number 0.25 needs 9-bits! Excess bits are truncated. Remember, we are only using 8-bits for the significand
0 10110 110010000
+ 0 10110 000000001
c)
// the revised version looks like this:
0 10110 11001000
+ 0 10110 00000000
0 10110 11001000
As such, the 0.25 gets truncated! We are left with just 100.
Exercise 74
Find the quotients and remainders for the following division problems with modulo 2.
This is rather simple. simply divide while making use of modulo 2 arithmetic.
In modulo 2 arithmetic, we get the following:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0
Here's an example of how to do it:
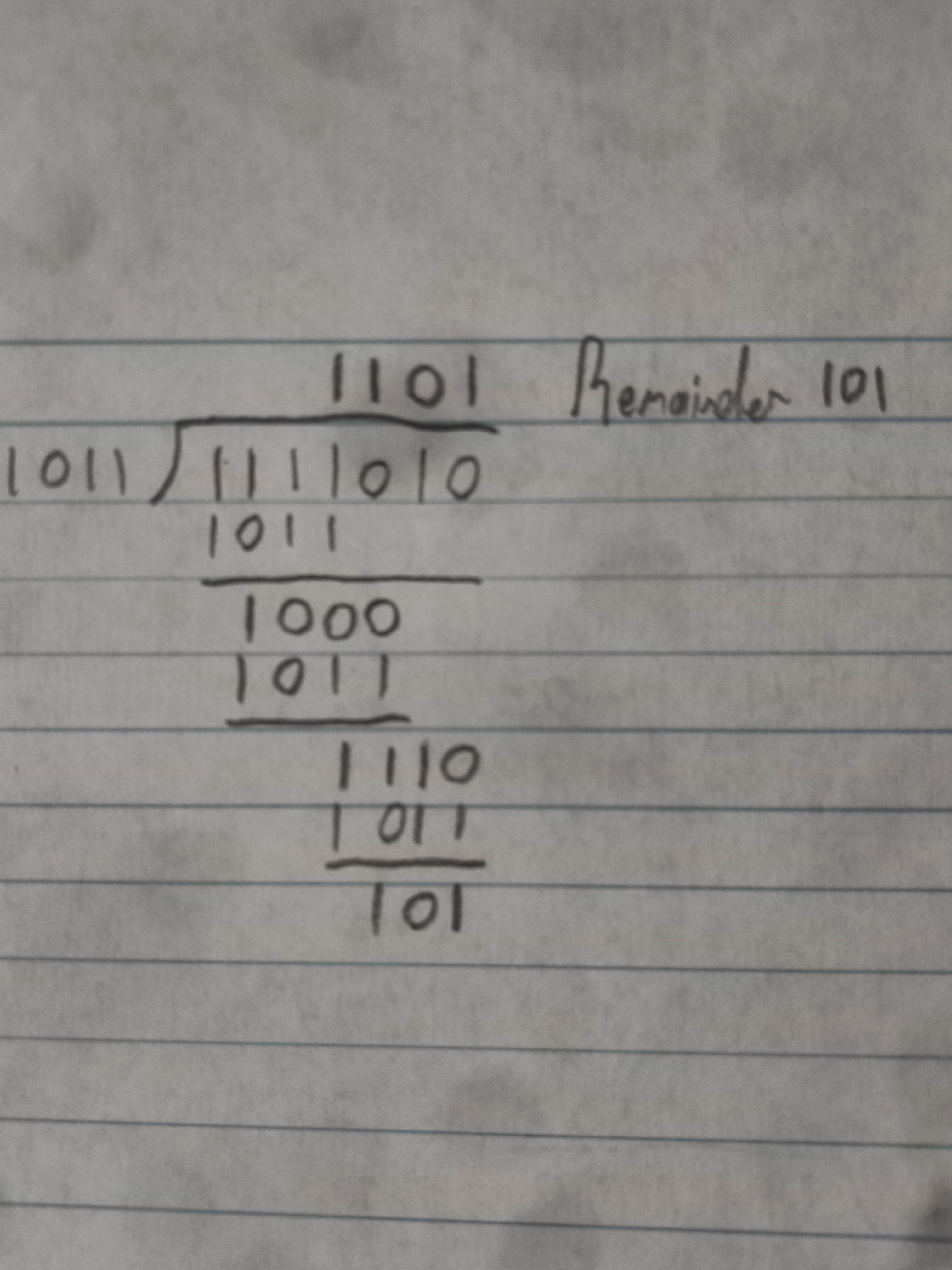
a) 11110102 / 10112 = 1101 Remainder 101
b) 10101012 / 11002 = 1100 Remainder 101
c) 11011010112 / 101012 = 111011 Remainder 1100
d) 11111010112 / 1011012 = 11010 Remainder 1001
Exercise 78
Using the CRC polynomial 1101, compute the CRC code word for the information word 01001101. Check the division performed at the receiver.
This one is rather easy. So then, note that 1101 has a total of four digits. Subtract 1 from that and append that many zeroes to 01001101. So then, 4 - 1 = 3 so append 3 zeroes so that we get 01001101000. Now divide!
010011010002 / 11012 = 1111100 Remainder 100
Add the remainder so that we get 010011010002 + 1002 = 010011011002
To show that everything works, divide 010011011002 by 11012. If the result has no remainder, then everything is well!
Answers:
interim quotient is 1111100 Remainder 100